
今回は、統計の基礎である「分散」と「標準偏差」について解説していきます!
分散や標準偏差は、統計検定3級でよく問われる範囲でもあり、また2級以上の学習の土台にもなるところです。
是非この機会にしっかり身につけておきましょう!
この記事を読むと分かること
- 標準偏差とは
- 分散とは
- 標準偏差と分散の違い

是非最後まで楽しんで読んでいただければ幸いです!
分散とは?
分散とは、データのばらつきを表す指標のことです。
具体的には、データ全体の平均からのズレ(データのばらつき)を数値化したものです。
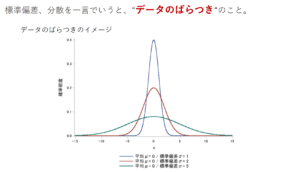
例えば、以下の図のように、各データと各値の乖離具合を調べていきます。
この乖離具合の合計が大きければ、ばらつきは大きいということが言えるかと思います。
ざっくりいうと、ばらつきとはそのようなイメージで、分散はそのばらつきの大きさを示した指標です。
データのばらつき
さて、ここからは具体的な例をもとに分散について解説していきます。
例えば、4人が受験したテストの点数が、それぞれ40、45,55,60だったとします。
この平均を出すと、50点となります。
次に、点数が0,0,100,100だったとします。
そうすると、この場合も平均点は50点となります。
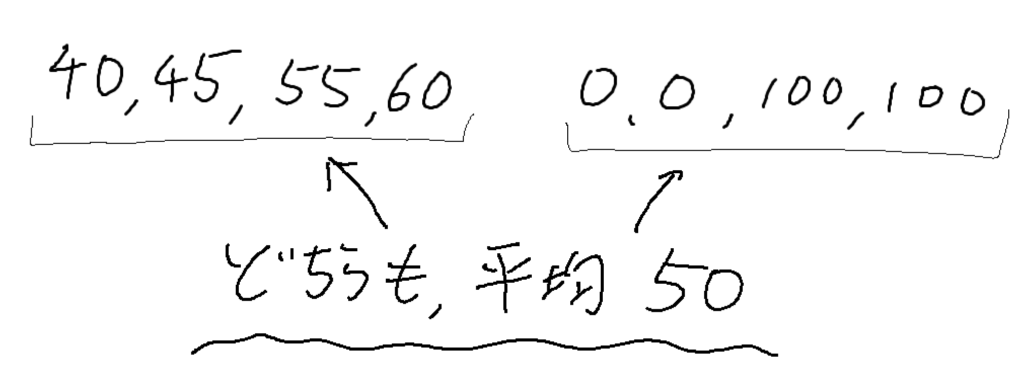
どちらも平均50点ですが、データの中身は全然違いますよね。
つまり、平均だけではデータがどれだけばらついているのかが分からないため、どれだけ平均を信用していいものなのか、よく分かりません。
そこで出てくるのが、データのばらつきを示す指標である分散なのです。
今回の場合は、おそらく0,0,100,100のグループの方が、ばらつきが大きそうな気がしますね。
実際に、分散でそのばらつきを数値化してみましょう!
分散の求め方
分散の求め方は、
一言でまとめると「平均からのズレ」の二乗の平均です。
公式にすると、以下の通りです。

これだけではよく分からないかもしれないので、
具体例を使って計算してみましょう。
以下の図を見てください。
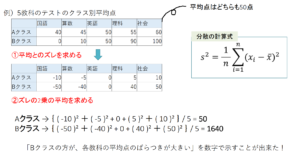
一見複雑そうな計算にみえるかもしれません。
しかし、実態としては以下の2つの計算をしているだけです。
- 平均とのズレを求める
- ズレの2乗の平均を求める
ちなみに、ズレを2乗している理由としては、そのままズレを足し引きした場合、プラマイ0になってしまうからです。
プラスのズレとマイナスのズレが相殺し合って0になってしまうのを防ぐために、2乗してマイナスをプラスに変えています。
難しそうに見えた分散の公式ですが、意味が分かれば、意外とシンプルに見えると思います。
分散の読み取り方
分散は、0に近ければ近いほどばらつきが小さいことを示しています。
そのため、今回のケースでは、
40、45,55,60のグループの分散が62.5
0,0,100,100の分散が2500 ということで
0,0,100,100のグループの方が分散が大きい(ばらつきが大きい)ということが分かります。
ばらつきの大きさを数値で表せるという点は非常に重要です。
分散の問題点
データのばらつきを表す指標として便利な分散ですが、分散には注意すべき点があります。
それは、計算の過程で単位が変わってしまうことです。
例えば、「5cm」を二乗すると「25cm2」になります。
つまり、数字を二乗すると、単位も同様に2乗されてしまうのです。
分散では、「平均とのズレ」の合計が0にならないよう2乗していました。
そのため、元データと異なる単位になってしまっているのです。
元のデータではcmの話をしているのに、「分散は~cm2となりました!」と言われたら少し違和感がありますよね。
その問題を解決した指標が「標準偏差」です。
標準偏差とは?
標準偏差は、分散同様データのばらつきを表す指標です。
ちなみに、標準偏差の「偏差」とは、平均とのズレのことです。
分散と標準偏差の違いは、標準偏差は分散の平方根であるという点です。
つまり、「標準偏差 = √分散」ということです。
前項では、分散は単位が変わってしまうため不都合が起きてしまうという話をしました。
単位を2乗したものを、元の単位に戻すために√をつけたものが標準偏差です。
√をつけることで、元のデータの単位に戻すことが出来ます。
標準偏差の公式は下の通りです。
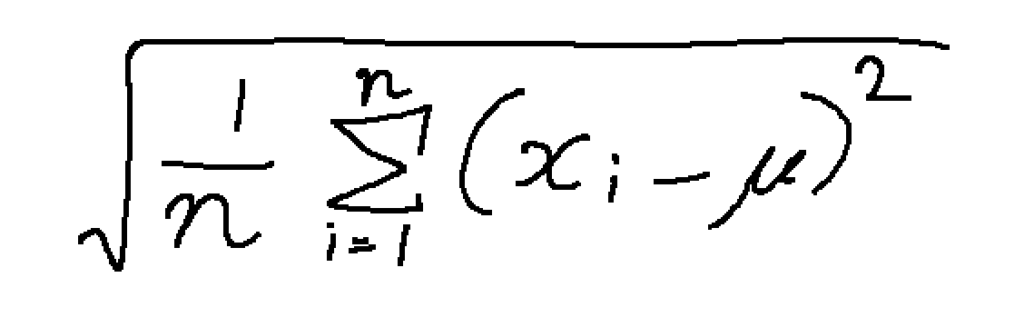
先ほどの例で、標準偏差を求めると、このようになります。
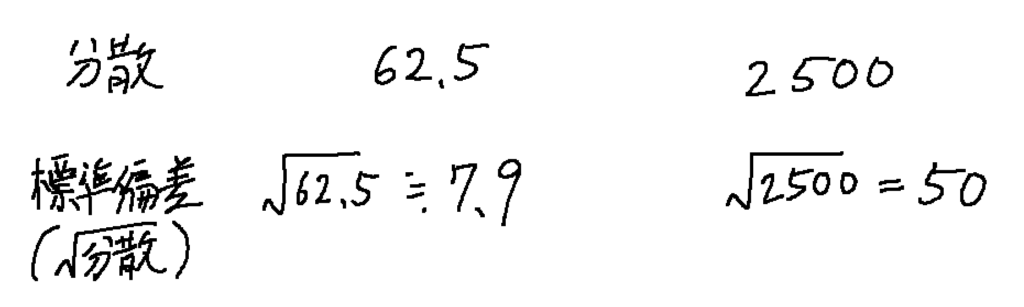
これで正しい単位のデータのばらつきの数値を求めることが出来ました。
まとめ
分散、標準偏差は、データのばらつきを表す指標です。
分散は「平均からのズレ」の二乗の平均、標準偏差は√分散 で求めることが出来ます。
分散や標準偏差は値が小さければ小さいほどばらつきが少ないということを表しています。
また、分散や標準偏差は、平均だけでは分からないデータのばらつきの大きさまで、読み取ることが出来るようになる非常に便利な指標です。
是非覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







