
こんにちは!統計ブロガーのにっしーです!
今回は、統計学のキホンを学ぶのに最適な統計検定3級を爆速で取るための重要事項をまとめてみました!
これを読むだけで統計検定3級に合格するためのキホンが一通り分かるようになります!
これから勉強する人のとっかかりや、受験直前の復習などで役立てていただければ幸いです!
統計検定3級ってどんな試験?
統計検定3級は、高校卒業までの数学知識を活用して統計活用力を評価する試験です。
加えて、基本的な統計調査の知識についても問われます。
そして、受験方法はCBT方式となります。
CBT受験というのは、テストセンターでパソコンを使って受験する方式のこと。
テストセンターさえ空いていればいつでも好きなタイミングで受験できるので、大変オススメです!
以前は、紙媒体で受験できるPBT試験もあったのですが、1級以外については2021年をもって廃止(全てCBT受験のみ)となりました。
統計検定3級に挑戦しよう!
統計検定3級は、全問選択式であり、一部常識的に分かる問題もあります。
また、2020年4月から合格点が70点→65点以上に変更され、より受かりやすくなりました。
ちなみに、合格率はおおよそ6~7割程度です。
ちゃんと対策をすればそれほど合格の難易度は高くありません。
是非この機会に取得しましょう!
統計検定3級は全て勉強しなくていい!
以下は、統計検定のHPの出題範囲を参考にまとめたものです。
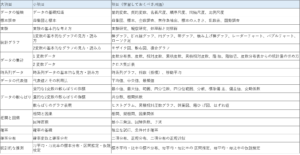
これをみると

と思うかもしれません。
しかし、ここには出題頻度が低い問題も含まれています。
また合格基準が65点以上ということで、こんなことをいうのもなんですが、ある程度間違えても大丈夫です。
何が言いたいかというと、統計検定3級は出題範囲を全て学ばなくても十分合格できる難易度の試験だということです。
出題範囲をみて、尻すぼみすることはありません。
実際、私自身統計検定3級に合格した時点では、「統計的な推測」の部分はほとんど理解していませんでした。
勿論、理解しているに越したことはありませんし、勉強しないことを勧めているわけでもありません。
しかし、出題範囲を完全に理解できていなくても、まずは挑戦してみるというのもアリだと思います。
統計検定3級の学習にオススメの参考書
用語の解説に入る前に、統計検定3級の学習にオススメの参考書を2冊だけご紹介します。
正直、ここで紹介する2冊さえあれば問題なく合格できます。
ネットをみると、いろんな方がいろんな本を紹介していて、「どれを買ったらいいのかわからない!」と思ってしまうかもしれません。
しかし、統計検定3級合格には、たくさんの参考書を買う必要はありません。
まず一冊目は王道中の王道、『統計検定3級公式過去問題集』です。
シンプルですが、過去問は解けば解くほどに合格率が上がっていきます。
なによりも手に入れておきたい1冊です。
こちらを試験当日までになるべく回数をこなしましょう。
また、以下の統計検定3級の公式テキストも手に入れておくと、万全です!
個人的な優先度的には過去問集>テキストですが、過去問集の解説を読んで分からなかった所をテキストでチェックすると言った活用方法がオススメです!
たくさんのテキストは必要ないので、最低限この2冊は持っておきたいところです。
統計検定2級の取得も視野に入れているなら
上記2冊でも統計検定3級の合格には十分ですが、2級受験の懸け橋になる1冊として、以下の書籍もオススメです。
私は、何冊もの統計入門書を読んでも理解しにくかった検定や推定、確率分布の部分が、この本のおかげで理解できるようになりました。
その結果、無事統計検定2級にも1発合格することができています。
「統計検定3級合格のあとは、統計検定2級も勉強して受験するつもりだ」という方に大変オススメの本です。
さて、前置きが長くなってしまいましたが、これより重要用語の解説を始めます!
赤字の部分は特に重要な箇所ですので、しっかり覚えるようにしてください!
データの種類

まずは、データの種類です。
データの種類は、大きく分けると以下の2種類があります。
データの種類
- 質的データ・・・分類項目であり、数量として意味ない
- 量的データ・・・数量として意味がある
質的データはあくまで分類そのもの。
たとえば、性別、血液型、星座、電話番号などですね。
これらに数量としての意味はありません。
例えば、電話番号が「090-xxxx-5342」「090-xxxx-7867」などがあったときに、「7867の方が数字が大きいから優れている!」ということはありませんよね。
これが、数量として意味がないということです。
一方、量的データには数量としての意味があります。
身長178cmは、165cmよりも大きいです。
気温16℃は気温25℃よりも低いです。
このように、量的データには数字の大小に意味があります。
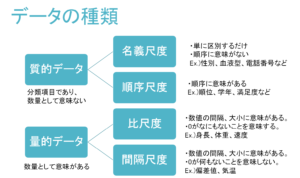
そして、質的データを細分化すると、名義尺度、順序尺度に分けることが出来ます。
また、量的データを細分化すると、比尺度、間隔尺度に分けることが出来ます。
これらの尺度について説明していきます。
尺度一覧
- 名義尺度・・・単に区別するだけ。順序に意味がない
- 順序尺度・・・順序に意味がある
- 比尺度・・・数値の間隔、大小に意味がある。0がなにもないことを意味する。
- 間隔尺度・・・数値の間隔、大小に意味がある。0が何もないことを意味しない。
名義尺度は単純な分類。
名義尺度の例としては、性別、血液型、電話番号などがあります。
順序に意味がないので、「A型の方がB型よりも優れている!」といったことはいえません。
一方、順序尺度は、その名の通り順序に意味があります。
たとえば、順位、学年、満足度などです。
「1位は3位より順位が上」
「6年生は2年生よりも学年が上」
「満足度5は満足度1よりも満足度が高い」などのように、順序に意味があるからです。
比尺度は比例尺度、比率尺度とも言います。
比尺度は、数値の間隔、大小に意味がありますが、0がなにもないことを意味するという特徴があります。
例えば、身長、体重、速度などが比尺度です。
身長cm、体重0kg、速度0kmはなにもありません。
一方、間隔尺度は、数値の間隔、大小に意味がある点は同じですが、0がなにもないことを意味しないというのが大きな特徴です。
また、数値の目盛りが等間隔であるという特徴もあります。
例えば、偏差値や気温なども間隔尺度の有名な例です。
偏差値0というのは偏差値がないことを意味しません。0という偏差値を意味しているからです。
(一般的に、偏差値は30~70くらいの値をとることが多いですが、理論上マイナスになったり、100をこえることも可能です。)
また、気温についても0度はなにもないわけではなく、0度という温度を意味しています。
(私たち人間が、たまたま水の凍る温度を0度と便宜的に決めただけなので。)
ここまでをまとめると以下のようになります。
このデータの種類については統計検定3級の序盤の問題で非常によく問われます!
しっかり覚えておきましょう!
グラフの種類
統計検定3級では、グラフの読み取りについても問われます。
出題範囲のグラフについて、特徴をそれぞれまとめてみました。
グラフの特徴
- 棒グラフ・・・単純な量の大小の比較に適したグラフ
- 折れ線グラフ・・・量の変化(推移)をみるのに適したグラフ
- 円グラフ・・・データ全体の中の構成比をみるのに適したグラフ
- 帯グラフ・・・データ全体の構成比の比較に適したグラフ
- 積み上げ棒グラフ・・・合計の度数の比較に適したグラフ
- レーダーチャート・・・複数の指標をまとめて確認するのに適したグラフ
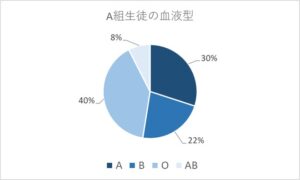
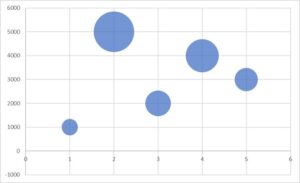
- バブルチャート・・・縦軸、横軸、点(バブル)の大きさで3種類のデータを表現する図。
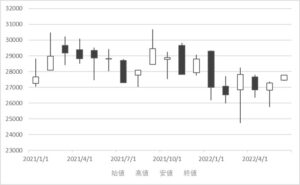
- ローソク足・・・値動きの推移を把握するのに適した図。FXや株価などの確認でよく使われる。
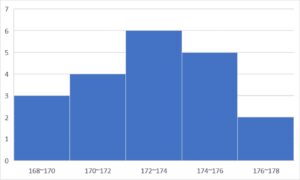
- ヒストグラム・・・データの散らばり具合を確認するのに適した図
- 散布図・・・2種類のデータの相関を確認するのに適した図。
各グラフについて概要を以下に載せておきます。
▼各グラフの詳細は以下の記事でもご紹介してますので、詳しく知りたい方はご覧ください!▼
【ビジネスマンなら知っておきたい!】統計グラフの種類・特徴一覧
棒グラフ・・・量の大小を比較
折れ線グラフ・・・変化の推移をみる
帯グラフ・・・構成比を比較
円グラフ・・・全体における構成比を確認
レーダーチャート・・・複数データのバランスや傾向を確認

積み上げ棒グラフ・・・累積データから内訳を比較
バブルチャート・・・3つのデータの関係性を確認
散布図・・・2つのデータの相関関係を確認
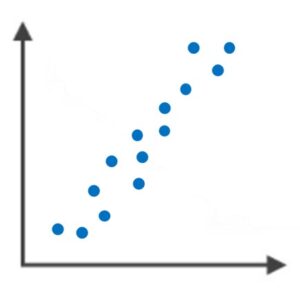
ヒストグラム・・・データの散らばり具合を確認するのに適した図
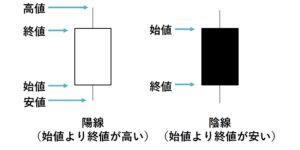
ローソク足・・・ 1日の取引時間中の株価の値動きを1本のローソクの形で表現
モザイク図・・・クロス集計表より、各層のデータを縦棒の積み上げグラフとして表現
統計調査について
さて、ここからは、統計調査について説明をしていきます。
暗記でとれる部分になってくるので、計算が苦手な方は特にしっかり覚えておくようにしてください!
全数調査と標本調査

統計検定3級では、統計調査の手法や基本用語についても問われます。
統計調査基本用語
- 母集団・・・調査対象となる全ての調査単位(世帯、企業、組織など)の集合
- 標本(サンプル)・・・母集団から選出した調査単位の集合のこと
- 標本抽出(サンプリング)・・・母集団から標本を抽出すること
- 無作為抽出(ランダムサンプリング)・・・ランダムに標本を抽出すること
- 全数調査・・・母集団の全ての調査単位を対象とする調査のこと 例)国勢調査、○○会社の全従業員の意識調査など
- 標本調査・・・母集団から抽出した標本を対象とする調査のこと 例)テレビの視聴率
全数調査と標本調査のイメージ
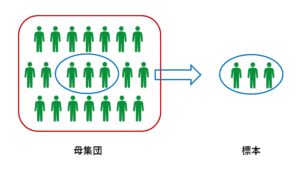
全数調査と標本調査の違い

全数調査の例はどれか、といった選択問題や、この調査はどの調査に該当するか、といった出題のされ方がありますので、ここもしっかり押さえておきましょう!
無作為抽出について
標本抽出の方法は、有意抽出と無作為抽出がありますが、統計検定3級では無作為抽出について問われます。
これはよく問われる部分なので、それぞれの無作為抽出の方法がどんなものかイメージはつかんでおくようにしてください!

無作為抽出について、なかなか文章だけでは伝わりにくいのでそれぞれ図解してみました!
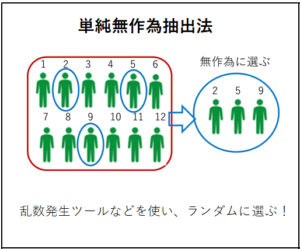
単純無作為抽出法・・・母集団すべてに番号を付けて、ランダムな方法で標本を抽出する方法。
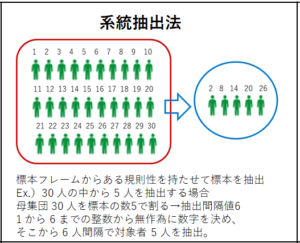
系統抽出法・・・標本フレームからある規則性を持たせて標本を抽出する方法。
集落抽出法・・・先に単純無作為、系統抽出法などにより調査を行う地域を決め、その地域の中に含まれるものを標本として抽出する方法。
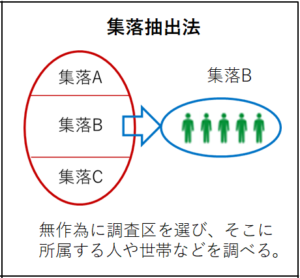
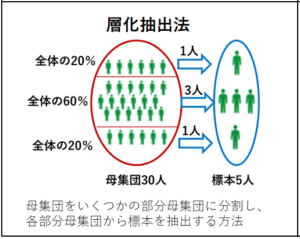
層化抽出法・・・母集団をいくつかの部分母集団に分割し、各部分母集団から標本を抽出する方法。
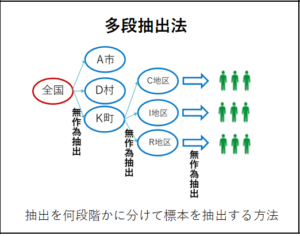
多段抽出法・・・抽出を何段階かに分けて標本を抽出する方法。抽出を二段階に分けて標本を抽出すると二段化抽出法となる。
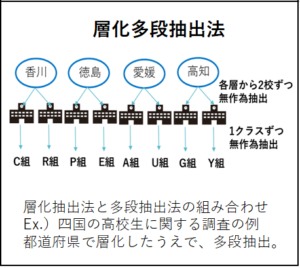
層化多段抽出法・・・層化抽出法と多段抽出法を組み合わせた方法。
度数分布表
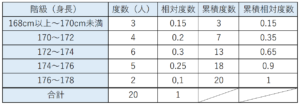
度数分布表は、データの最小値から最大値までの間をいくつかの階級に分類し、それぞれの階級に含まれる度数を示した表のこと。
具体的には、以下のような表が度数分布表です。
なかには累積度数や累積相対度数が載ってないものもあったりしますが、それらも度数分布表です。
度数分布表の各用語を説明します。
度数分布表基本用語
- 階級・・・データを整理するために用いる区間
- 階級の幅・・・区間の幅
- 階級値・・・階級の真ん中の値
- 相対度数・・・「各階級の度数」÷「度数の合計」
- 累積度数・・・その階級以下の度数を全て合計した値
- 累積相対度数・・・「累積度数」÷「相対度数」or 「その階級以下の相対度数を全て合計した値」
度数分布表を使ってデータを整理すれば、データ全体の中で、どの部分のデータ数(度数)が多いのか、が簡単に把握できるようになります。
このデータの階級値はどれか、という出題も多いです。
上記の度数分布表でいうと、「176~178」の階級値は、177です。
知っていればすぐ解ける、かつ出題頻度も高いので、しっかり押さえておいてください!
ヒストグラム
度数分布表と合わせて問われやすいのがヒストグラムです。
というのも、ヒストグラムは、度数分布表の内容をより直感的に把握しやすくするためにグラフ化したものだからです。
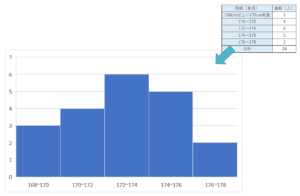
ヒストグラムを使うことで、データの分布を直感的に把握することができます。
また、ヒストグラムでは、横軸にデータの値をとり、縦軸に度数を取ります。
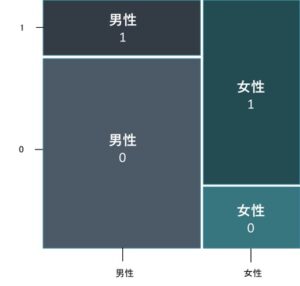
クロス集計表
クロス集計表は、2つのカテゴリーに属するデータを、それぞれのカテゴリーで分類し、データ数を集計できる便利な表です。
具体的には、以下のようなものがクロス集計表です。

性別というカテゴリーと、好きな教科というカテゴリーそれぞれのデータ数(度数)が一目で確認できます。
上記のようなグラフは、左側の性別のカテゴリーが2つ、上側の教科のカテゴリーが5つなので、
2×5のクロス集計表
という言い方をします。(カテゴリーの数によって変わります。)
統計検定3級では、クロス集計表から読み取れる情報の正否がよく問われます。
しっかり度数分布表の読み取り方についても理解しておきましょう!
代表値
代表値とは、データ全体の特徴を表す(代表する)値のことです。
具体的には、以下の3種類に分かれます。
代表値の種類
- 平均値
- 中央値
- 最頻値
それぞれの要点をまとめると、以下の図の通り。
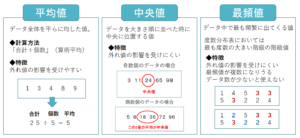
それぞれについても解説していきます。
平均値
平均値は、その名の通り、データ全体を平らに均した(ならした)値のことです。
私たちが小学生のころに習ってきた、「合計÷個数」の一般的な平均(正確には「算術平均」という)のことです。
平均値は、データ全体を使って導き出す代表値だという特徴があります。
そのため外れ値の影響を受けやすいというデメリットがあります。
※外れ値とは、他の値から大きく離れた値のこと。
例えば、年収100万円のフリーター4人の中に年収1兆円を超えるといわれているビルゲイツが1人加われば平均年収は爆上がりします。
このように平均値は外れ値に弱い側面があります。
中央値
中央値は、データを大きさ順に並べた時に中央に位置する値のことです。
中央値は、データが奇数個の場合はシンプルに真ん中に位置するデータを選びます。
偶数個の場合は、真ん中に近い2つのデータの平均が中央値となります。
図にすると、以下の通りです。
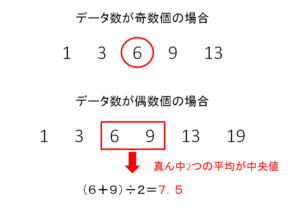
中央値の特徴は、外れ値の影響を受けにくいことです。
先ほどの例で、年収100万円のフリーター4人の中に年収1兆円を超えるといわれているビルゲイツが加わったとしても中央値は変わりません。
特に、データが偶数個の場合の中央値は問われやすいです。
しっかり押さえておきましょう!
最頻値
その名の通り、最頻値は最も頻繁に観測される値のことです。
こちらも中央値同様、外れ値の影響を受けにくいという特徴があります。
一方、データ数が少ないと活用できない(しにくい)、最頻値が複数になる可能性もあるというデメリットもあります。
※度数分布表においては、最も度数の大きい階級の階級値が最頻値となります。
四分位数、四分位範囲
四分位数とは、データを大きさ順に並べた時に、データを4等分する値のことです。
言葉では伝わりにくいところなので図を見てみましょう。
データを大きさ順に並べて4等分というのは以下のようなイメージです。
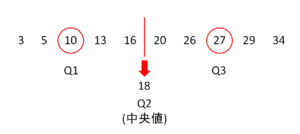
データの順番がバラバラの場合は、まず並び替えをするところから始まります。
ちなみに四分位数は
- 第1四分位数・・・Q1
- 第2四分位数・・・Q2
- 第3四分位数・・・Q3
と表すことも多いので覚えておきましょう。(Qはquartileの略)
※第二四分位数は中央値と同じ意味です。
また、データのばらつき度合いをはかる指標の一つとして、四分位範囲があります。
四分位範囲はデータの約半分がどれだけの範囲にあるのかを確認できる指標です。
計算方法は以下の通り
四分位範囲 = 第3四分位数 ー 第1四分位数
また、四分位偏差という値もあり、計算方法は以下の通りです。
四分位偏差 = 四分位範囲 ÷ 2
特に四分位範囲はよく問われるので覚えておきましょう!
箱ひげ図
箱ひげ図とは、データのばらつき具合や5数要約を直感的に把握できる図のことです。
※5数要約・・・最小値、第一四分位数、中央値、第三四分位数、最大値のこと。
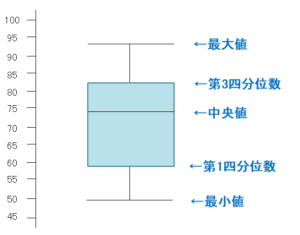
ちなみに、統計学では「範囲 = 最大値 ー 最小値」で求めます。
箱ひげ図の読み取りは、非常によく問われます。
特に、「表のデータを箱ひげ図で的確に表したものはどれか」といった問われ方や、「箱ひげ図を読み取って、正しい記述を選ぶ」という問われ方も多いです。
また、実際の試験では、一つの箱ひげ図でなく以下のように複数の箱ひげ図を比較しながら読み取るようなパターンが多いです。
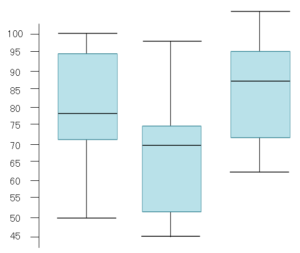
まずは、箱ひげ図の読み取り方をしっかり押さえて、過去問でトレーニングをしておきましょう!
標準偏差、分散
標準偏差、分散を一言でいうと “データのばらつき“ のことです。
データのばらつきとはなんなのかという点も含めて身近な例で考えてみましょう。
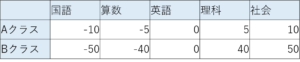
例)5教科のテストのクラス別平均点
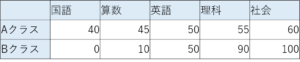
こちらの表を見る限り、なんとなくBクラスの平均点の方がばらついているのは分かると思います。
しかし、相手にデータのばらつき度合いを示すときに「みたらわかるじゃないですか!」では非常に説得力に欠ける主観的な解釈だと思います。
そんなときに、ばらつきの度合いを数値で客観的に表せるのが分散や標準偏差なのです!
標準偏差、分散の求め方
まず分散の計算方法は以下の通りです。(「平均からのズレ」の二乗の平均)
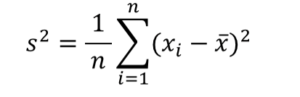
一見難しそうな式ですが、要は以下の2つの計算をしているだけです!
- 平均とのズレ(偏差)を求める
- ズレの2乗の平均を求める
平均とのずれを求めているのは、「ばらつきの度合いを知るためには、平均値との乖離具合の合計を求めればばらつきの大きさがわかるんじゃね?」というイメージです。
また、偏差を二乗しているのは、プラスマイナスが相殺しあって0になるのを防ぐためです。
さて、実際に先ほどのテストの例で計算してみましょう。
まずは、「①平均とのズレを求める」です。

平均点はどちらも50点です。上記点数から50点を引いてみましょう。
そうすると、以下のようになりました。
次に、「②ズレの2乗の平均を求める」をしていきます。
Aクラス→{(-10)²+(-5)²+0+(5)²+(10)²}/5 = 50
Bクラス→{(-50)²+(-40)²+0+(40)²+(50)²}/5 = 1640
そうすると、Aクラスの分散は50、Bクラスの分散は1640となり、「Bクラスの方がばらつきが大きい」という事実を数字で示すことが出来ました!
これがデータのばらつきを数値で示すということです。
標準偏差と分散の違い
さて、標準偏差と分散はどちらも同じばらつき度合いを表す指標ですが、一体何が違うのでしょうか。
それは、標準偏差は分散の平方根ということです。
標準偏差の計算式は以下の通りです。
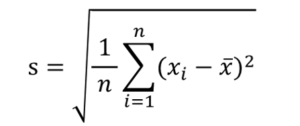
さきほどの分散の計算式に√をつけただけですね。
でもなぜ分散に√を付けただけの指標がわざわざあるのでしょうか。
その理由は、標準偏差には分散のデメリットをなくす特徴があるからです。
分散は、計算の過程で2乗していますね。
そのため、単位も変わってしまうというデメリットがあります。
例えば、身長(㎝)の話をしているのに、分散を求めると㎝²になってしまいます。
そうすると、イメージもつきにくいし違和感も残ります。
そのため、「分散に平方根を付けたら元の単位に戻せるやん!」という考えで出来たのが標準偏差なのです!
標準偏差は現在多くの場所で活用されており、身近なところでは学力の偏差値の計算にも標準偏差は活用されています。
相関係数
相関係数とは、2変数間の関連の強さを数値化したものです。
計算式は以下の通り。
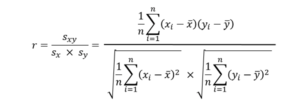
文字がたくさんあってややこしそうな式ではありますが、よくみると意外とシンプルです。
xとyの共分散 ÷ xの標準偏差×yの標準偏差 ということです。
試験では、共分散や標準偏差はすでに問題文で示されていることが多いので、まずは計算式だけ覚えておきましょう。
相関係数の特徴
相関係数の読み取り方はかなり頻出です!絶対に覚えておきましょう!
相関係数の読み取り方
- 正の相関が強いと相関係数が1に近づく
- 負の相関が強いと相関係数が-1に近づく
- 相関係数が1 又は-1 のときは完全相関という
- 相関係数が0 の付近は相関がないといえる
「正の相関がある」というのは、「気温が上がると、アイスが売れる」といった比例のような関係のイメージです。
逆に、「負の相関がある」というのは、「気温が上がると、おでんが売れなくなる」といった反比例のような関係です。
また、相関係数1や-1は完全な相関なので、グラフで表すと完全な直線になります。
つまり、相関係数が-1や1に近いほど、散布図上のデータが直線に近い形になっていきます。
このイメージも覚えておきましょう。
相関についての注意点
相関関係=因果関係ではないという点に注意が必要です。
例えば、アイスクリームの売り上げと、水難事故には相関関係があります。
というのも、ここには第三の変数として、気温が関係しています。
アイスクリームは気温が高いほど売れやすくなります。
また、気温が高いほどプールや海に行く人が増えるので水難事故も増えます。
その結果、アイスクリームが売れるにつれて水難事故増えているように見えてしまうのですが、実際のところ因果関係(アイスクリームが売れたから水難事故が増えたというわけではない。逆もしかり)はないのです。
このように、相関係数が高くなるため因果関係がありそうに見えるが実際には関係がないようなものを擬似相関(擬相関)といいます。
(名前のせいで少しややこしいのですが、疑似相関でも相関関係はあるので、イメージとしては「疑似因果」のほうが正しいと思っています。。)
変動係数
変動係数は、2つの異なるデータのばらつきの度合いを表す指標です。
計算式は以下の通りです。
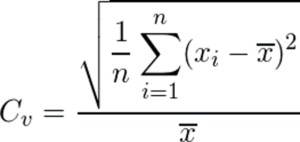
一見ややこしそうに見えますが、要は「標準偏差 ÷ 平均」ということですね。
いたってシンプルです。
変動係数は以下のような場合に活躍します。
例1 単位が異なる場合
- 身長 : 平均 170cm 標準偏差 4.6cm 変動係数0.027
- 体重 : 平均 61kg 標準偏差 2.8kg 変動係数0.045
身長と体重は、単位が異なるため単純に標準偏差の大小で比較が出来ません。
このような場合に変動係数が役に立ちます。
上記例の変動係数をみると、体重の方が値が大きいので、すなわち体重の方が身長よりもばらつきが大きいということいえます。
例2 平均値が異なるケース
- 管理職の年収 : 平均年収 2000万円 標準偏差 450万円 変動係数 0.225
- 一般社員の年収 : 平均年収 300万円 標準偏差 100万円 変動係数 0.33
一般社員の平均年収は管理職の平均年収に比べて平均値が小さいため、単位が同じでも標準偏差の単純比較では適切な解釈が出来ません。
上記例では、標準偏差の値のみ見ると管理職の方がばらつきが大きいということになります。
しかし、変動係数を求めると、実は一般社員の方がばらつきが大きいといえることが分かりました。
最後に
あとは統計検定3級合格には高校レベルの確率の基礎がわかっていればおおよそ大丈夫です。
確率に自信がない方は以下の記事をご覧いただければと思います。
条件付き確率については下記記事をご確認いただければと思います。
統計検定2級超頻出テーマ「条件付き確率」の問題を簡単に解くとっておきの方法!
また、統計的推測については以下の記事を読んでいただければ理解がしやすいです。
区間推定における信頼区間とは何か 特徴や求め方について分かりやすく解説
ただ、個人的には3級の取得では統計的推測まで理解していなくても合格できると思っています。
(私自身統計的推測をほぼ分かっていない状態で、統計検定3級には合格できました。)
検定や推測はつまずきやすい部分であり、かつ3級ではそこまで大きな得点を占める部分ではありません。
なので、まずはその他の部分を完璧にすることが大切だと思います。
当ブログのなかには統計検定3級の用語に関するブログがたくさんありますので、是非色々読んで勉強してみてください!
最後まで読んでいただきありがとうございました!







