
今回のテーマは、四分位数です。
「四分位数」ということばは、平均値などとは違って、なかなか日常生活では聞き慣れないことばだと思います。
しかし、統計検定3級でもかなり頻出のテーマであり、また統計学の基礎として重要な範囲でもあります。
是非、この機会に覚えておきましょう!
この記事を読むと分かること
- 四分位数とは
- 四分位範囲とは
- 四分位偏差とは

是非最後まで楽しんで読んでいただければ幸いです!
四分位数とは
四分位数(しぶんいすう)は、データを大きさ順に並べた時に、データを4等分する値のことです。
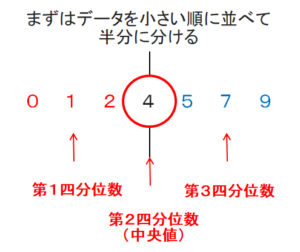
その4等分する値を小さい方から順番に、以下のように呼びます。
- 第一四分位数(=小さい方から25%の位置)
- 第二四分位数(=中央値)(=小さい方から50%の位置)
- 第三四分位数(=小さい方から75%の位置)
英語では四分位数のことをQuartileと言うため、その頭文字をとって、それぞれ第一四分位数をQ1、第二四分位数をQ2、第三四分位数をQ3と表すこともあります。
また、第二四分位数は中央値と同意ですので、ここもしっかり覚えておきましょう。
四分位範囲
冒頭で、四分位範囲はその範囲にデータの半分が含まれているということを示す「ばらつきの指標」の一種と述べました。
これをより具体的にいうと、第一四分位数から第三四分位数までの範囲のことを指します。
つまり、「第三四分位数 − 第一四分位数」で求めることができます。
四分位範囲では、以下のようなことを言えます。
- 大きければ大きいほど、データのばらつきが大きい
- 小さければ小さいほど、データのばらつきが小さい
データの範囲自体は、最大値から最小値を求めれば出すことができますが、もしその中に一つだけとびぬけて大きいデータ(外れ値など)が含まれていたら、その影響を大きく受けてしまいます。
具体的に考えてみましょう。
たとえば、「1,2,3,4,5,6,7,8,100」というデータがあったとします。
この場合、100は外れ値となります。
ここで、「最大値-最小値」でデータの範囲を求めると、「100 - 1 = 99」となります。
ほとんどは8以下なのに、99になってしまうと、データ全体の特徴をうまく表現しているとはいえません。
そこで四分位範囲が役に立ちます。
同じデータについて四分位範囲を求めると、以下のように、四分位範囲は4となります。
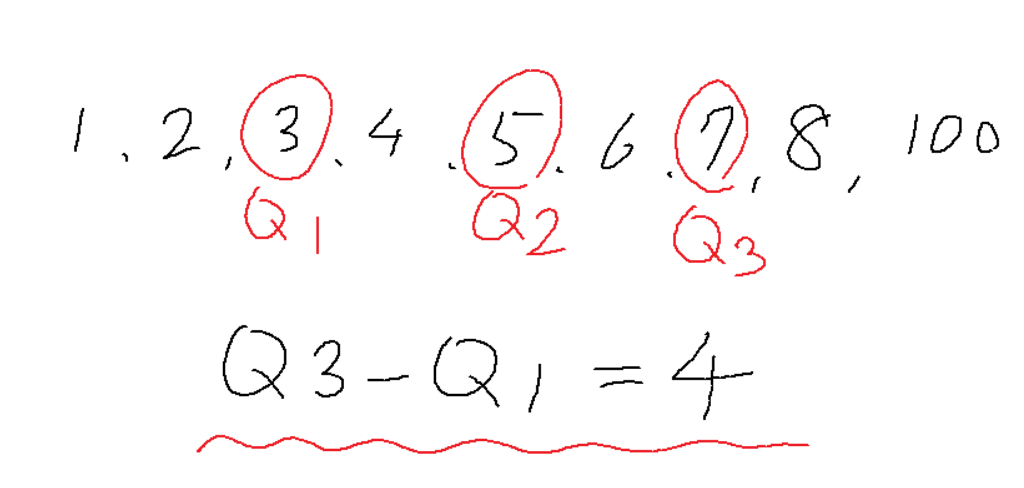
このように、外れ値がある場合のばらつきを表す指標として、四分位範囲は有効です。
四分位偏差
四分位偏差は、データのばらつき具合を示す指標です。
求め方としては、(第三四分位数 - 第一四分位数) ÷ 2 です。
つまり、四分位範囲 ÷ 2 です。
読み取り方についても、四分位範囲と同様で以下のようなことがいえます。
- 大きければ大きいほど、ばらつきが大きい
- 小さければ小さいほど、データのばらつきが小さい
これだけ聞くと、「四分位範囲と何が違うの?」「なんで2で割ったの!?」と思う方もおられるかもしれません。
「四分位範囲」はQ3-Q1です。
この「四分位範囲」 を 2で割ると、その値がQ2(中央値)と比べてどの程度差があるのかを確認することが出来るようになります。
この点が、四分位範囲と四分位偏差の違いです。
四分位数、四分位範囲、四分位偏差の意義
四分位数が分かることで、四分位範囲と四分位偏差を求めることが可能になります。
四分位範囲は、その範囲にデータの半分が含まれているということを示す「ばらつきの指標」の一種です。
また四分位偏差は、偏差と言う位なので、こちらもデータのばらつき具合を示す指標の一つです。
分散や標準偏差、平均偏差など、データのばらつきを示す指標はほかにもありますが、
その中でも四分位範囲、四分位偏差を利用するメリットとしては、外れ値の影響を受けにくい指標であるという点です。
このように、四分位数を求めることは最終的に、データのばらつきや偏りの度合いを把握することにつながっていくということですね。
また、四分位数は、箱ひげ図を作成するときにも利用される値です。
箱ひげ図については、以下の記事をご覧ください。
箱ひげ図とは 正しい読み取り方やExcelでの作成方法とともに解説
まとめ
四分位数を求めることで、四分位範囲や四分位偏差などの外れ値に近いばらつきの指標を求めることができるようになります。
また、四分位数は、箱ひげ図というばらつきの指標を表したグラフを作成するときに必要となる値です。
全体の散らばり具合を知りたいときは、分散や標準偏差を使い、外れ値が含まれているデータのばらつきを見たいときは四分位範囲や四分位偏差を使う、といったように、目的に応じて指標を使い分けていきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







