
いきなりですが皆さんは「偏差値」をご存じでしょうか。
よく模試の結果を確認するときや、受験先を決める際の指標として使われることが多いため、多くの人が聞いたことのある言葉だと思います。
しかし、「具体的に偏差値ってなんなのか」「どのようにして求められているのか」という話になると、答えられる方は多くはないと思います。
そこで今回は、「偏差値とは何なのか」「どのようにして求められているのか」など、偏差値について具体的に解説していきたいと思います。
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- 偏差値とは
- 偏差値の求め方

今回の説明の中で、「標準偏差」という言葉が出てきます。
この言葉にピンと来ない方は、まず標準偏差について説明した以下のブログを読んでから見ていただけると、より分かりやすいと思います。
最後まで楽しんで読んでください!
偏差値とは
まず、偏差値の定義は以下の通りです。
学力などの検査結果が、集団の平均値からどの程度へだたっているかを示す数値。
デジタル大辞泉
つまりは、自分の点数が全体の中でどのような位置にあるのかを相対的に読み取るための指標といえるでしょう。
偏差値の求め方
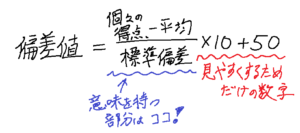
偏差値は、「(自分の得点-平均値)を標準偏差で割って、 10 倍し、それに 50 を加える」計算で求まります。
こちらを式にすると、以下の通りです。

ちなみに、偏差値の公式の後ろについている(+50) と(×10) の部分は、
結果を読み取りやすくするためだけの数字です。
私たちは、テストの成績など、100点満点基準で考えることが多いですよね。
そのため、偏差値-15、偏差値10とかになるよりも、それらに50を足した偏差値35、偏差値60などの方が見やすいと感じる方が多いと思います。
また、「×10」をしなかった場合、値が小さすぎて差がよく分からないということになってしまう可能性があるので、10をかけてるだけです。
このように、この(+50)や(×10)のところは、あくまでも結果を見やすくするための調整ということで、数学的な意味は一切ありません。
そのため、偏差値として意味を持つ部分は、(個々の得点ー平均)÷標準偏差の部分だけなのです。
これで偏差値を計算するうえで重要な部分もお分かりいただけたかと思います。
偏差値の読み取り方
先述の通り、偏差値は自分の点数が全体の中でどのような位置にあるのかを相対的に読み取るための指標です。
偏差値では、真ん中である 50からどれだけ離れているかで、自分が全体の中でどれくらいの位置にいるのかを把握することができます。
例えば、「50より大きければ、真ん中より上の成績(中央値以上)」「50よりも小さければ、真ん中よりも下の成績(中央値以下)」などが偏差値から読み取ることができます。
また、一般的には、「偏差値60で全体の上位16%」「偏差値70で全体の上位2.3%」と言われているので、こちらも目安の一つになります。
同じ点数でもテストによって偏差値が違う理由
皆さんは、以下のような経験をしたことはないでしょうか。
そして今回のテストでも70点だったのに、今回は偏差値は62だった。
なぜ同じ点数なのに、テストが違うと偏差値も変わるのだろう・・・。
なぜこのようなことが起こってしまうのか、その答えは偏差値の求め方にあります。
あらためて偏差値の公式をみてみましょう。

偏差値の公式のなかには、平均と標準偏差が含まれています。
テストによって、受験人数や受験者の点数がそれぞれ変わってくるため、データをならした値である平均や、ばらつきの指標である標準偏差の値も当然変わってきます。
そのため、同じ点数だったとしても計算に含まれる平均や標準偏差が異なるため、テストによって偏差値も変わってくるという仕組みになっているのです。
偏差値の取りうる範囲
偏差値の取りうる範囲には、特に制限はありません。
リアリティには欠けますが、理論上は 100を超える偏差値や、逆にマイナスの値を取ることも可能性としてはあります。
たとえば、100人がテストを受けて、99人が0点、1人が100点だったとします。
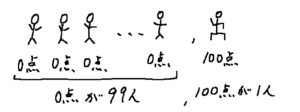
このデータをもとに考えると、以下のように計算することができます。
- 平均点:1点
- 分散:99
- 標準偏差:3√11 ≒ 9.95
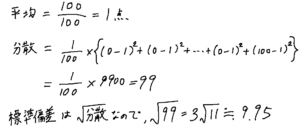
ここから100点の人の偏差値を求めると、「10×(100‐1)÷9.95+50=149.49・・・」となり、軽く偏差値100を超えます。

実際、過去に偏差値100超えの実例もあるようです。
ただ、このようなことはなかなか起こりません。
多くの場合は、偏差値は20~80くらいに収束することがほとんどです。
まとめ
偏差値は、平均や標準偏差を加味した指標です。
そのため、テストが違っても、自分がどれくらいのレベルにいるのかを相対的に把握できます。
この機会に是非覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





