
この記事を読むと分かること
- 信頼区間ってなに?
- 信頼区間の特徴や求め方

統計の勉強を進めていくと、「推定」「信頼区間」という言葉をよく目にするようになるかと思います。
その言葉から、何かを推測するものだということは分かるかもしれません。
しかし、具体的に何を推測するのか、どのように推測しているのか、本当に上手く推測できていると言えるのか、など色々な疑問が出てきて、「よく分からない」と感じる方も少なくないかもしれません。
今回は、統計学の中でも重要な分野に位置づけられる「推定」に着目し、区間推定に必要な信頼区間の特徴や求め方について解説していきたいと思います!
是非最後まで読んでみてください!
信頼区間は区間推定における超重要指標
推定とは?
まず、そもそも「推定」とはどのようなものを指しているのでしょうか?
推定とは、母集団の平均や分散といった「真値」と呼ばれる値を、母集団から取り出した標本のデータから推測していくことを言います。
母集団全体を調査してその平均や分散を求めることができれば一番良いのですが、母集団の数が何百万、何千万と増えていくと、全てを調査することは難しいですよね。
そこで母集団から標本をいくつか取りだして、その標本の平均や分散から母集団の平均や分散を推測していこうというのが推定です。
推定には「点推定」と「区間推定」という2つの手法がありますが、今回は基本的な「区間推定」に着目していきたいと思います。
信頼区間とは?
区間推定は、ある区間の中に真値が含まれるだろうということを標本のデータから推測していく推定手法の1つです。
母集団から取り出した一部のデータである標本の情報から、真値はこれだ!と1つに絞ることはなかなか難しいので、ある程度の範囲まで絞ることで、母集団の真値を予測するのが区間推定の特徴です。
では、その「ある範囲」というのはどのように求めていけば良いのでしょうか?
それが、今回詳しく解説していく「信頼区間」という指標です!
信頼区間の算出によって上限と下限を決めることで、その範囲に真値が含まれるだろうということが推測できるようになります。
信頼区間の求め方
信頼区間の求め方にはいくつかのパターンがあります。
なかでも、今回は母集団が正規分布に従っていると仮定し、母集団の平均である母平均が分かっている場合に限定して、信頼区間を求める手順を紹介していきたいと思います。
例として、男子高校生の平均身長について考えてみましょう!
男子高校生の身長の平均に対する信頼区間
今回は、全国の男子高校生を母集団として、身長の平均をと明らかにしたいと思います。
しかし、全国の男子高校生の身長を全員調査するのは難しいと思います。
そこで、あるクラスの男子9人の身長から、母集団の身長の平均である母平均を区間推定しようと思います。
あるクラスの男子9人の身長を調査した結果は以下の通りでした。
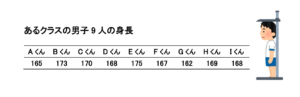
ここで、母平均に対する95%信頼区間は「標本平均±1.96標準偏差/√n」で表すことができます。
今回の例では、平均は168.6、標準偏差3.91、標本の大きさnは9となるので、あるクラスの男子の身長から推定した全国の男子高校生の身長の平均の信頼区間はこのように計算されます。
- 168.6 – 1.96×3.91÷√9 = 166.0 ←95%信頼区間下限
- 168.6+1.96×3.91÷√9 = 171.1 ←95%信頼区間上限
以上より、身長の母平均に対する95%信頼区間は、[166.0, 171.1]の範囲となります。
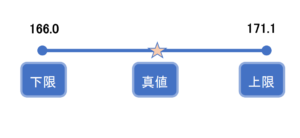
信頼区間を求める式さえ押さえておけば、簡単に算出することができますね!
1.96の意味とは?
ところで、信頼区間を求める式の中に1.96という数字がありましたが、この1.96とはいったいどこから来ているのでしょうか?
今回の例では正規分布に従うことを仮定しているのですが、この正規分布の性質が1.96と深い関わりを持っています。
正規分布の山の頂上である平均を中心として、左右に標準偏差1.96個分を取った範囲は分布全体の95%を占めることから1.96という数字が来ています。
95%信頼区間の場合は「標準偏差/√n」の部分に1.96をかけますが、90%信頼区間や99%信頼区間など、どこまでの範囲を許容するかによってかける値は変わってくるので注意しましょう。
正規分布の性質について詳しく知りたい方、復習したい方は以下の記事を読んでみてください。
信頼区間の特徴
信頼区間の求め方について、身長の例を用いて解説しましたが、信頼区間の上限と下限の値に大きな差があると、「真値はここだ!」と確信をもって言いづらいですよね。
そこで、信頼区間の精度が上がるための条件という観点から、信頼区間の特徴について2つ紹介していきたいと思います。
標本の大きさが大きいほど推定精度が良くなる
1つ目は、標本の大きさが大きいほど推定精度が良くなるという特徴です。
95%信頼区間の計算式をもう一度見てほしいのですが、標本の大きさnは「標準偏差/√n」の分数の分母にあたる部分に存在しています。

この分母にあたる部分が大きくなればなるほど、分数全体の大きさが小さくなります。
分数全体の大きさが小さくなれば、「標準偏差/√n」で表されている誤差の部分も小さくなるので、信頼区間の幅が狭くなり、精度が良くなるというわけです。
標準偏差が小さくなれば推定精度が良くなる
2つ目は、標準偏差が小さくなれば推定精度が良くなるという特徴です。
1つ目の特徴につながる部分もあるのですが、標本から得られたデータのばらつきが小さいということが分かれば、標準偏差/√nの値も小さくなります。
その結果、先ほどの1つ目の特徴と同じように、平均±の後ろの誤差全体が小さくなって推定精度が上がります。
標準偏差/√nのことを「標準誤差」と呼ぶのですが、標準誤差の大きさを小さくすれば信頼区間の幅が小さくなるので、標準誤差を小さくするための条件がこの2つということになります。

信頼区間の意味を正しく理解しよう!
95%信頼区間の求め方や信頼区間の特徴については理解したけれども、信頼区間そのものの意味についてはこれまで詳しく紹介していませんでした。
なぜなら、信頼区間の意味を間違って解釈している人が非常に多いからです!
文章で意味の違いを説明しても違いが分かりにくいと思うので、図を用いながら少し丁寧に解説していきたいと思います。
95%信頼区間の意味を間違えている人は、このように解釈している場合が多いのではないでしょうか。
「求めた信頼区間の中に95%の確率で真値(母平均や母分散)が含まれる」
実は、この解釈は間違いです。
正しい信頼区間の解釈はこのようになります。
「母集団から標本を取ってきて何度も信頼区間を求めた時に、95%の確率で信頼区間の中に真値が含まれる」
やはり文章だと違いが分かりづらいですね。
下の図を見てもらうと少しわかりやすくなるかもしれません。
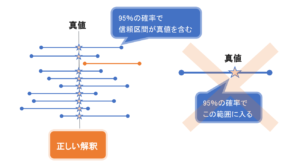
間違った解釈では、信頼区間を固定したうえで、母集団の母平均や母分散といった真値がいろいろな値を取るという意味になってしまいます。
一方で正しい解釈は、母平均は1つに定まっていて、その母平均を推測するときの信頼区間をたくさん求めても、5%の確率で母平均が信頼区間の中に含まれないことがあるということになります。
「真値は1つしかない」ということを念頭に置いておくと、正しい解釈ができるようになるかもしれませんね。
まとめ
今回は母集団の真値を推測する手法の1つである「区間推定」に着目し、区間推定を行ううえで重要な「信頼区間」という指標について詳しく紹介しました。
信頼区間の正しい求め方を学ぶだけではなく、正しい意味を理解して、真値を推測できるようになりましょう!
※信頼区間についてより詳しく知りたい人は以下の記事も読んでみてください!
視聴率の計算方法を知っていますか?視聴率で学ぶ標本調査の仕組み







