
今回は、統計検定2級で定番の条件付き確率の解き方について解説していきます。
ほぼ毎回出題されている範囲なので、この機会にしっかり押さえておきましょう!
この記事を読むと分かること
- 条件つき確率の問題を解く方法

最後まで楽しんで読んでいただけますと幸いです!
問題
2019年11月の問8(解答番号12,13)を見ていきましょう。
問題は、こちらから↓
http://www.toukei-kentei.jp/wp-content/uploads/201911grade2.pdf
(一般財団法人 統計質保証推進協会 統計検定公式HPより)
解説
文章だけで考えると、頭がこんがらがって少し分かりにくい問題です。
かといって、「P(A∩B)などの記号はよく分からない!」という方もおられるかもしれません。
ちなみに、公式の過去問題集の解説はこのような記号を使った解説が多く、数学が苦手な方にとっては少しとっつきにくいかもしれません。
しかし、この手の問題はこんな記号を使わなくても簡単に解ける方法があります!
それは、中学校の確率でも習った、樹形図を使って解く方法です!
事象を列挙
まずは問題文をしっかり読んで、どんな事象があるのかを書きだしていきます。
実際に読んでいくと、どうやら以下の事象に分類できそうだということが分かります。
事象
- 対策講座を受講した or していない。
- 検定試験に合格した or していない。
つまり、パターンとしては、2通り×2通りなので、以下の4通りに分かれます。
ポイント
- 対策講座を受講して、検定に合格
- 対策講座を受講して、検定に合格していない
- 対策講座を受講せず、検定に合格
- 対策講座を受講せず、検定に合格していない
樹形図を書く
さて、事象が分かったら、今度はこれらについて樹形図を書いていきます。
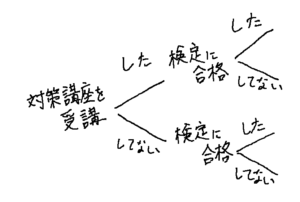
続いて、樹形図の枝のところに、問題文にある確率を書き足していきます。
確率では、1=100%なので、30%は「0.3」といったように記載していきます。
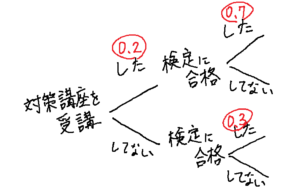
これが問題文から分かる確率です。
そして、確率は1がMAXなので、対策講座を受講した人の確率が0.2であれば、対策講座を受講していない人の確率は「1-0.2=0.8」ということが分かります。
同様に、検定に合格したかどうかについても確認していきます。
それらの確率を全て書き足していくと、以下の通りになります。(青字の箇所)
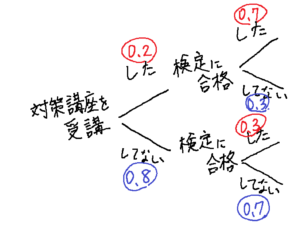
確率を計算
ここまで分かれば、あとは簡単です!
それぞれの確率を求めていきましょう。
対策講座を受講し(0.2)、検定に合格した(0.7)人である確率は、0.2×0.7=0.14 (14%)となります。
同様にして、4通り全ての確率を求めていくと、以下の通りになります。
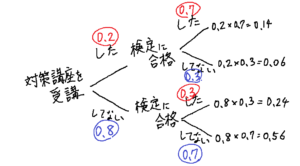
簡単な計算をして終わり!
さて、問題文を改めて確認してみましょう。
解答番号12は、 「検定試験を受験した人から無作為に1人選んだとき,その人が対策講座を受講した合格者である確率」なので、上で求めた0.14がそのまま答えとなります。
選択肢でいうと、①が正解です。
解答番号13は、検定に合格した人の中で、講座を受講した人である確率。
これは、
ポイント
(講座を受講した&検定に合格した) ÷ 検定に合格した人全体
で求めることが出来ます。
つまり、計算式は以下の通りです。
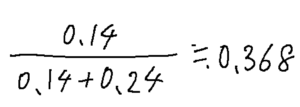
選択肢を見ると、③に0.37があるので、こちらが答えとなります!
最後に
2級は、後半に行くにつれて、検定などの難しめの問題が増えてくるので、この確率での2問は落としたくないところです。
過去問を見ても、この解き方で条件付き確率の問題は解けてしまう問題がほとんどです。
また、条件が追加されたら、そのぶん枝の数を増やしていくだけなので、応用も利きます。
難解な式を使わずに解けるので、覚えておくと非常に便利です!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







