「統計学」という言葉は、かなり広義かつ大きな括りなので、細かく分類することができます。
なかでも有名な分類方法として、「記述統計学」と「推測統計学」という分類方法があります。
「記述統計学、推測統計学ってそれぞれどういう意味なの?」
「何が大きな違いなの?」
そのような疑問に答えるべく、今回は”記述統計学と推測統計学の違い”について簡単に説明します!
記述統計学とは

記述統計学とは、観測データの特徴を捉えるための学問です。
観測データとは、ざっくりいうと手元にあるデータのことです。
記述統計学では、母集団の推測は行わず、あくまで観測データの分析がメインです。
記述統計の例を挙げると、以下のようなものがあります。
記述統計の例
- 国勢調査や人口調査
- 勉強時間と偏差値の相関分析
- 全国模試の偏差値
- ビッグデータを用いた売上データの分析 etc..
「模試の結果から平均点や偏差値を出す」
「会社の1ヶ月の売上データをグラフ化し、分析する」
これらは経験したことがある人も多いのではないかと思います。(偏差値を算出する側はあまりないかもしれませんが・・・)
「記述統計」というお堅い言葉で聞くと難解な気がしますが、
実はかなり身近なもので、多くの人が記述統計だと認識せずに記述統計の考え方を使っているのです。
データをもとに表やグラフを作成して、データの特徴を探るのも記述統計学の一種。
そのほか、平均や分散、相関係数などを用いて、データの特徴を分かりやすくすることも記述統計の役割です。
たとえば以下のようなデータがあったとします。
A高校男子テニス部10人の身長データ(cm)
160,174,176,171,165,179,174,168,175,168
ばらばらで少し見にくいですよね。
そのため、度数分布表とヒストグラムにしてみましょう。
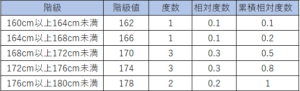
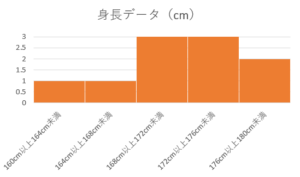
図や表を作るだけで、かなり特徴が捉えやすくなりましたよね。
さらに、もっとデータの特徴を分かりやすくするために、平均と標準偏差も計算してみましょう。
すると、以下のような計算結果となります。
- 平均 → 171cm
- 標準偏差 → 約5.46
算術平均と加重平均の違いとは それぞれの特徴や具体例を解説!
これでただの数字の羅列のように見えたデータの特徴が読み取りやすくなりました。
このデータの特徴を分かりやすくするためのテクニックこそが記述統計です。
推測統計学とは

推測統計学は、一部(標本、サンプル)のデータを使って全体(母集団)の特徴を推測する学問です。
最近話題の「ベイズ統計」は、実は推測統計の一種です。
たとえば、テレビの視聴率は推測統計の例として有名です。
テレビの視聴率を算出するために、テレビを持っている日本中の全ての世帯からデータを取るというのが非現実的だというのはなんとなくイメージがつくと思います。
そのため視聴率は、地区ごとに一定数の家庭からデータをとり、それぞれ視聴率を予測しています。
つまり、一部から全体を予測しているので、視聴率は推測統計となるのです。
▼詳しくは以下の記事で解説しています!▼
そのほかの推測統計の例をあげると以下のようなものがあります。
推測統計の使用例
- 選挙の当確速報
- 保険会社が利用する事故発生数予測
- 新薬の有効性判断
- モノづくりにおける不良品の発生数予測 etc...
今や、私たちの周りには数え切れないほどのデータがあふれています。
そのため何かを分析しようと思ったときに、それに関する全てのデータを収集して分析することが難しい場合もあります。
むしろ莫大な時間やコストをかけるくらいなら、標本調査で十分だというケースだって往々にしてあります。(まさに視聴率もその一つです。)
例えば、あなたがとあるアンケートを行うことになったとします。
アンケート対象者の母集団は100万人。
実際に100万人にアンケートをとって調査データを集めるのは大変そうな気がしますね。
しかし、これが1000人なら、大変かもしれませんが、まだなんとかなる気がしませんか。
でも、「1000人だったら100万人とは全然違うし、不十分な分析結果になるんじゃ・・・」と思うかもしれません。
実際その通りで、どうしても母集団から一部(標本)を取り出した調査では、母集団の結果とズレが出てしまいます。
(この標本を抽出したことによる誤差を「標本誤差」といいます。そのままですね。笑)
なのでそんなときは、「あくまで100万人のうちの1000人なので、これくらいの誤差は考えられます。これくらい信頼できる分析結果です!」と言うことを示すことが出来れば、それで問題ないのです。
実際、100万人の母集団に対し標本が1000人あれば、上下誤差3%程度という精度の高い分析が出来ます。
このように、母集団が大きい場合に活躍するのが推測統計の考え方なのです。
まとめ
今回は、記述統計と推測統計の違いについて解説しました。
簡単にまとめると、以下の通りです。
- 記述統計は、観測データを分析する統計であり、
- 推測統計は、標本を抽出し、それらをもとに母集団(全体)の姿を予測する統計ということです。
どちらも私たちの身近なところで大活躍している考え方なので、覚えておくと非常に便利です。
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





