
「今話題沸騰中のあのドラマが、なんと視聴率○○%を記録しました!」
そんな話を誰もが一度は耳にしたことがあると思います。
しかし、具体的に「視聴率がどのようにして求められているのか」まで知っている人はそう多くないと思います。
実は、テレビの視聴率は統計学を利用して算出している身近な例の一つなんです。
今回はそんな、視聴率と統計学の関係についてお話しをしたいと思います。
視聴率の仕組み
視聴率は、ビデオリサーチ社が開発したビデオメーターと呼ばれる自動計測器を使って計測されています。
具体的には、無作為に選ばれた数百世帯の家庭(「モニター世帯」といいます)のTV受像機に取り付けられた自動計測機が、電源のオンオフや、視聴しているチャンネルについての情報を自動で集計するというシステムです。
PMメーターというものを使うと、世帯視聴率だけでなく、世帯内の4歳以上の家族の中で、いったい誰がどのくらいテレビをしたのかということまでわかるようです。
視聴率は1分ごとに調べられ、これを毎分視聴率と呼びます。
この毎分視聴率の合計を番組の放送時間で割ることで、私たちがよく聞く平均視聴率が算出されるのです。
視聴率は標本調査
視聴率は、数百世帯から収集されるデータから算出されています。
視聴率が全世帯から集計されているわけではないことは有名ですが、「まさかそんなに少なかったなんて!」と思う方もおられるかもしれません。
視聴率調査のように、母集団の中からいくつかを標本として抜き出し、そのデータをもとに母集団の特徴を推定していく方法のことを標本調査といいます。
視聴率でいうと、母集団はテレビを持っている全世帯。
標本は、無作為に選ばれ自動計測機を設置されたモニター世帯のことですね。
モニター世帯の選ばれ方~系統抽出法~
せっかくなので、視聴率の調査対象となるモニター世帯がどのようにして選ばれているのかもご説明します。
ビデオモニター社は、「系統抽出法」という方法を使ってモニター世帯を選んでいます。
系統抽出法は次のような手順で行われます。
- 母集団全てに通し番号をつける。
- どのくらいの間隔をあけて標本を選んでいくか決める。
- 最初の一つの標本だけを無作為に選ぶ
- 選ばれた標本から一定間隔をあけて、通し番号順に選んでいく
たとえば、母集団が1000世帯として、最初に選ばれた6番の標本から、5ずつ間隔をあけて選んでいく。
そうすると、6 , 11 , 16 , 21 , 26 ・・・
と選ばれていくというわけです。
こうして無作為に選ぶことで、標本が偏った性質のものばかりになることを避けているのです。
視聴率はたった数百世帯から計算されている!?
日本における視聴率の計測は、
テレビの放送エリア32地区でそれぞれ調査されています。
地区によって調査世帯数は異なり、それぞれ
- 関東地区 → 900世帯
- 関西地区、名古屋地区 → 600世帯
- 北部九州 → 400世帯
- その他の地区 → 200世帯
という世帯数で視聴率を計算しています。
※2020年3月30日より世帯調査数が変わるようです。本記事最後の追記をご確認ください。
関東地区の世帯数は約1800万世帯といわれていますが、実際に1800万世帯から調査をするのは、時間もコストもかかり、現実的ではありません。
そのため、標本抽出して調査対象である900世帯からデータを収集して分析しています。
1800万世帯のうちの900世帯ということは、関東地区の世帯数全体のたったの0.005%程度ということになります。
かなり小さい気がしますよね。
「本当にたったこれだけの数で視聴率が分かるのか・・・?」と思う方もおられるかもしれません。
しかし、統計学に基づいて考えると、900世帯でも関東の視聴率データの全体像をある程度予測することが出来るのです。
「ある程度」といったのは、視聴率の計算には誤差の範囲が含まれているからです。
標本調査には誤差がある!
標本調査には、誤差があります。
なぜなら、母集団から一部を抜き出した標本で調査をしているため、母集団全体で調査したときと比べると、調査結果に差が生まれるからです。
この誤差のことを標本誤差といいます。
少ない標本でも十分な理由
なぜ、たったの0.05%の世帯から集めたデータで、関東地区の視聴率を予測できるのか。
実際に計算しながら考えてみましょう。
正規分布の性質から、視聴率の標本誤差は以下の式で求めることができます。
サンプル数をn、視聴率をp、信頼区間を95%とすると、 ±1.96√p(1-p)/n
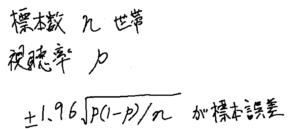
それでは次に、具体的な数字を当てはめてみましょう。
標本数を900世帯、視聴率が20%、信頼区間95%とします。
そうすると、次のように計算できます。

このように、視聴率20%!と言われていても、
実際は、95%の確からしさで17.4%~22.6%の値をとるよ~ってことなのです!
次に、標本数をうんと増やして1万世帯に変えてみましょう。
そうすると、計算結果は以下のようになります。

1万世帯に増やしても、19.2%~20.8%という誤差の範囲は生じてしまうのです。
仮に1万世帯も調査するとなると、それだけで自動計測器の準備やコスト、その他もろもろの手間がかなり増えます。
はたしてそこまでしてまで、この誤差を埋める必要があるのか。
そう考えたときに、関東ならば900世帯もあれば十分だろう、と調査地区によって誤差の許容範囲と調査会社の負担を考慮して調査世帯数は決められているのです。
サンプルを増やせば、誤差は小さくなる!
標本調査では、サンプル数が多ければ多いほど、推定値の区間幅は狭まります。
別の言い方をすると、より正確な推定ができる、誤差の幅が小さくなるとも言えますね。
なんとなくイメージはつくかもしれませんが、「なぜサンプルを増やせば誤差は小さくなるのか」についても簡単に説明します。
サンプルを増やす=母集団に近づく
サンプル数を増やすということは、そのぶん元の形(母集団)に近づいていくということです。
標本を抽出するからこそ標本誤差が生じるのであり、
母集団全てを調査すれば、標本誤差はありません。
関東地区の視聴率も900世帯からのデータをもとにしているので誤差がありますが、1800万世帯全てからデータを収集すれば誤差はなくなりますよね。
そのため、サンプル数を増やせばデータの元々の全体の形に近づいていき、誤差が小さくなるということです。
標本誤差の式から考えてみる
さきほどの式からも標本誤差の式からもサンプルを増やすと誤差が小さくなる理由がわかります。
たとえば、標本数が100の場合と、2500の場合を考えてみましょう。
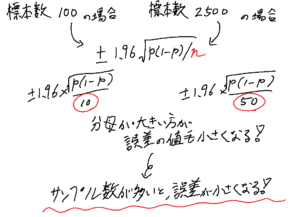
そうすると上のように、1.96にかける値が分母が大きいほど小さくなるので、誤差も小さくなるということです。
これが、サンプル数が多いと誤差も小さくなる仕組みなのです。
録画やネットワーク視聴も視聴率に入る?
最近では、様々なVOC(ビデオ・オン・デマンド)によってコンテンツを視聴する方々も増えてきました。
まだ研究段階ではありますが、ビデオリサーチ社は今後こういったネットワーク視聴などについても対応出来るように対応デバイスを広げていくような認識を持っているようです。
デジタルシフトの流れに合わせて、視聴率調査についても求められることが増えているということでしょう。
(参考)https://www.itmedia.co.jp/lifestyle/articles/1212/05/news133.html
最後に
最後まで読んでいただきありがとうございます。
視聴率がここまで密接に統計学と関わっているというのは意外だったのではないでしょうか。
このような例は、視聴率だけでなく身近なところでもたくさんあります。
たとえば内閣支持率の計算なども標本調査の代表例としてよく挙げられますね。
しかし、そんな標本調査には誤差があるということはわすれてはなりません。
視聴率が20%といわれても、実際は17%台や22%台であることもあるのです。
データを見るときは、全数調査なのか、標本調査なのか、標本調査ならば誤差はどの程度なのかなどを意識してみると、街中で見る様々なデータを見る目が変わるかもしれません。
追記(視聴率調査の変更)
ビデオリサーチ社のHPを調べてみると、どうやら2020年3月30日より世帯調査数が変わるなど、調査設計を変更するようです。
本記事で言及した世帯調査数に関していうと、
- 関東:900世帯 → 2700世帯
- 関西:600世帯 → 1200世帯
- 札幌:200世帯 → 400世帯 のように変わるとのこと。 (https://www.videor.co.jp/press/images/tvrating_release_1.pdf)
サンプル数が増えるということは、より誤差の小さい正確な視聴率を出すことができるようになるということです。
今後も視聴率は、どんどん信頼性の高いものになっていくことでしょう。
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







