
こんにちは!統計ブロガーのにっしーです!
今回は代表値の一種である平均についてのお話です。
代表値に関する知識は、統計検定3級を取得する際に必須ですので、是非この機会に覚えておきましょう!
▼代表値については、以下の記事で詳しく説明しています!▼

平均には、一般的に用いられる算術平均の他に、加重平均、幾何平均、調和平均があります。
そのなかでも今回は、「調和平均」について解説していきます。
▼算術平均、加重平均、幾何平均につきましては、以下の記事をご覧ください▼
算術平均と加重平均の違いとは それぞれの特徴や具体例を解説!
調和平均とは
調和平均(harmonic mean)は、平均の速度を計算するときによく用いられる平均のことです。
調和平均は、「各データの逆数の算術平均の逆数」で求めることが可能です。
式にすると、以下のようなイメージです。
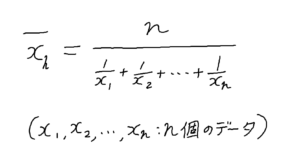
式だけ見てもなかなかイメージがわきにくいと思いますので、具体的にどのような場面で利用されるのか詳しく見ていきましょう!
調和平均の例
具体例①移動速度の計算
例えば、以下のような例題があったとします。
例題1
Aさんは、毎日自宅と会社を往復している。
ある日Aさんは寝坊したので、行きは時速10kmで走って向かった。
帰りは、いつも通り時速5kmで歩いて帰った。
このとき、行きと帰りの平均速度は時速何kmになるか。
ここで、時速10kmと時速5kmの平均だから、(10+5)÷ 2 = 7.5、
つまり、「平均速度は時速7.5kmだ!」と算術平均で求めてしまうと、コレは間違いです。
なぜなら、速度が違うため、移動時間もそれぞれ異なるからです。
調和平均を用いた正しい計算方法がわかれば、その意味も分かると思います。
まず、「自宅~会社」間の距離を「dkm」とおいてみることにしましょう。
そうすると、往復で移動した距離は「2dkm」となります。
続いて、行きと帰りの移動にかかった時間を考えてみましょう。
ここで使うのは、小学生の時に習った「キハジ」(もしくは「ミハジ」「ハジキ」など)の計算式です。
「時間 = 距離 ÷ 速度」
この式から、
- 行きにかかる時間は d/10 時間
- 帰りにかかる時間は d/5 時間
と計算することができます。
また、先ほどの式を変形すると、
「速度 = 距離 ÷ 時間 」
なので、ここから以下の計算ができます。
平均時速 = 2d ÷ (d/10 + d/5)≓ 6.67
よって、平均時速は約6.67kmというのが答えになります。
具体例②仕事の速さの計算
せっかくなのでもう一つ、よく使われる調和平均の例があるのでご紹介します。
時速以外では、仕事の速さを考える問題でも調和平均は利用されます。
たとえば、以下のような問題です。
例題2
ある作業をAさんが行うと3日かかる。
Bさんが行うと6日かかる。
では、二人で取り組めば何日で終わるか。
俗にいう、仕事算の問題ですね。
よく見るこの形式の問題も、実は調和平均の問題なのです!
まずは、それぞれの一日あたりの作業量を考えます。
全体の作業量を1とした場合、
Aさんは3日かかるので、一日あたりの作業量は1/3となります。
同じように、Bさんは6日かかるので、一日あたりの作業量は1/6です。
つまり、二人で取り組んだときに一日に進む作業量は、1/3と1/6を足し合わせれば出てきます。
計算すると、
1/3 + 1/6 = 1/2
のようになります。
ここから、二人で取り組めば一日で全体の作業量の1/2(半分)進むということが分かるので、
「二人で取り組めば2日で終わる」というのが解答になります。
まとめ
小中学校でみたことのあるような問題が、実は調和平均だったのだと知ると、少し意外だったかもしれません。
特に2つ目の仕事算の例題は、実際にビジネスの場面でも活用できそうなので、是非覚えておいてください!
これまで「平均」と聞いても、1種類しか思い浮かばなかった方も、今では平均に複数の種類があり、場面によって、「算術平均、加重平均、幾何平均、調和平均」を使い分けることが重要だと実感してもらえたのではないでしょうか。
是非、使うべき平均を正しく見極めながら、実生活に活かしていってください!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







