今回は、データ分析の現場でも非常によく使われる基本的な統計手法の一つである「相関分析」について詳しくご紹介していきます。
是非この機会に知識を身につけておきましょう!
この記事を読むと分かること
- 相関分析とは
- 相関係数の特徴
- 相関係数の計算方法
- 相関係数の読み取り方
- 相関係数の注意点
- 散布図との関連性
- 相関分析の利用場面

最後まで楽しんで読んでいただけますと幸いです!
相関分析とは
相関分析とは、2つのデータにおける関係性の強さを分析する手法です。
「定量データ×定量データ」の2つのデータの間の関連性を見る場合に用いられます。
相関分析と聞くと、「相関係数」という指標を思い浮かべる方も多いと思いますが、「相関係数」は相関分析のアウトプットの指標の一つになります。
相関係数の特徴
相関とは、2つの変数のデータ対が一直線上にのるような関係がある場合、2つの量的変数が完全に関連していることを表します。(=相関がある)
直線からの逸脱の度合いが強まるにつれ、変数間の関連性(相関)は薄くなる、ということです。
簡単にいうと、気温が上がれば、ビールがよく売れる、といったような比例・反比例の関係の強さを示します。
この場合、ビールと気温には相関関係がある、といういい方をします。
相関係数の計算方法
相関係数の計算方法は以下の通りです。
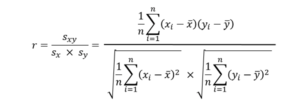
計算式で見ると難しいそうですが、要は xとyの共分散 ÷ xの標準偏差×yの標準偏差 ということです。
二変数の標準偏差で共分散を割っているのは、共分散が変数の単位に依存して変化してしまうのを修正するためです。
※共分散・・・それぞれ2変数の平均からの差の席の和をデータ数で割ったもの。共分散は平均から見て2つの変数がどういった傾向を示すのかというようなことを表現する式になります。
このように、分子である共分散がどういった傾向を示している変数なのかを理解すると、相関係数がどのようにして二変数間の関連性を表しているのかを理解することが出来ます。
相関係数の読み取り方について
相関係数の範囲は、ー1~+1を取ります。
相関係数の強さは、0の値から絶対値が1に近づくにつれて相関の強さが強くなるということを示し、-1であれば負の相関、+1であれば正の相関ということになります。
相関係数が0の場合は無相関である、変数間に直線的な関連は一切存在しないということになります。
相関係数の評価の目安は以下の通りです。
- 0.0<|r|<0.2 ほとんど関係がない。0.0は無相関
- 0.2<|r|<0.4 弱い関連がある
- 0.4<|r|<0.7 中程度の関連がある
- 0.7<|r|<1.0 強い関連がある
ただし、これらの評価基準は絶対的な基準ではありません。
使われる場面や目的によって読み取り方は変わるため、あくまで一般的な目安として利用するようにしてください。
相関係数の注意点
相関係数には、利用するうえでの注意点がいくつかあるので、ご紹介します。
因果関係のない相関(見かけの相関)がある
相関係数を利用する際の注意点として、相関係数の絶対値が1に近くても、2つの変数の間に関連があるとは言い切れない場合があるということです。
そのような相関は以下のようなものがあります。
- 見かけの相関 第3の変数による見かけの相関
- 擬似相関:第3の変数の影響で、相関係数が見かけ異常に大きくなる。
- 擬似無相関:第3の変数の影響で、2変数間の相関関係が見かけ上無相関になる。
例えば、アイスクリームの売上と熱中症患者数には相関がありますが、「アイスが売れたから熱中症になった!」というわけではありません。
アイスの売上が上がったのも、熱中症患者が増えたのも、それぞれ気温が影響しています。
暑ければアイスはよく売れますし、熱中症になる人も増えます。
このように相関係数だけ見ると高くても、実際には2変数間には関連がない場合もありますので、2つの変数間の相関を見るときには、第3の変数の影響を除いた上で考えなければなりません。
疑似相関や見かけの相関についての具体例は以下の記事でたくさん紹介していますので、もっと知りたいと思った方は是非読んでみてください!
疑似相関(見せかけの相関)の具体例11選!~警察官が増えると検挙数が増える!?~
ちなみに、第3の変数の影響を取り除いた相関係数のことを偏相関係数といいます。
数学的に言うと、「xとyの相関係数を見るときに、zからの影響をコントロールしたもの」というイメージです。
先述の見かけの相関のように、第3の変数が邪魔をしているケースがあるので、2つの変数間の相関を考える際は、第3の変数からの影響も考慮して考えなければなりません。
直線以外の関連も考えられる
例えば、紅茶、コーヒーなどの美味しさと温度で調査をすると、曲線の相関があるとになると予想されます。
(これらの飲み物は、熱いか冷たいものが好まれて、ぬるいものはあまりおいしくなさそうだと思います。)
このように、非線形関係の相関がある場合も考えられるため、正しく二変数間の関連を調べる際は相関係数だけではなく、散布図とあわせて考えることが重要になってきます。
相関係数は外れ値の影響を受ける
相関係数は、外れ値の影響を受ける指標です。
なぜなら、相関係数は計算式の一部に平均を含んでいるからです。
※相関係数の求め方は、以下の通り。

平均値は外れ値の影響を受ける指標であるため、その平均を使って計算している相関係数も外れ値の影響を受ける指標だということです。
平均値について、詳しくは以下の記事をご確認ください。
そのため、相関分析をする際には、データに外れ値がないか確認することも重要です。
床面効果と天井効果
変数の取ることが出来る範囲に制限があると、相関係数に影響が及ぶこともあります。
これを天井効果、床面効果といいます。
例えば、0点~100点のテストがあったときに、本来もっと実力があるのに100点満点のために100点までの点数しかとることができないようなことを天井効果といいます。
逆に、どんなに勉強しなくても0点よりも下の点数は取りようがないようなことを床面効果といいます。
相関係数を活用する際には、床面効果、天井効果の影響も考慮することが大切です。
切断効果
切断効果とは、データの一部を取り出すと相関係数が変わってしまうことを意味します。
例えば、100点、80点、60点、40点、20点の5人の点数があったときに、5人の平均をとると60点になります。
しかし、標本調査で一部だけ取り出して調査することになったとします。
そこで、100点、80点、60点の人だけを取り出してしまうと、平均は80点になります。
平均が変わるということは、そのデータを使って別のデータとの相関係数を取ろうとすると、相関係数も変わってしまいます。
偏った範囲のデータしか得られていないといったことがないか、データ分析の際には注意することが必要です。
散布図との関連性
相関係数は、散布図から読み取った相関の程度を表す指標でもあります。
散布図だけでは、説明変数と目的変数の具体的な相関の強さまでは読み取れません。(おおまかには分かりますが。)
そこで、実際に関連の強さを表す相関係数を用いて、二変数間の相関の強さを数値で示します。
そうすることで、関連の強さを数値によって表現することができます。
Excelを使って分析してみよう ~CORREL関数~
Excelの関数であるCORREL関数を使用して相関分析を行います。
CORREL(コーレル)関数は、相関という意味をもつCORRELATION(コリレーション)からきています。
これからCORREL関数を使用して分析する3つの方法を説明します。
例として、最高気温とビールの売り上げについての相関分析を行います。
セルに直接、関数を手入力する方法
1つ目の方法は、セルに直接、関数を手入力する方法です。
①セルにカーソルがある状態で、「=co」と入力すると、COから始まる関数の一覧がプルダウンで表示されます。
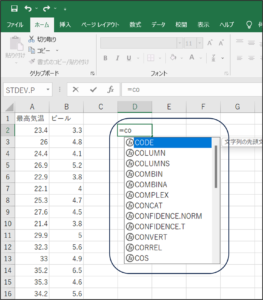
②下矢印で「CORREL」までフォーカスを移動させ、Tabキーを押します。
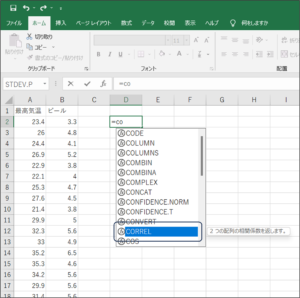
③CORREL関数で比較したいデータの入力待ち状態となります。
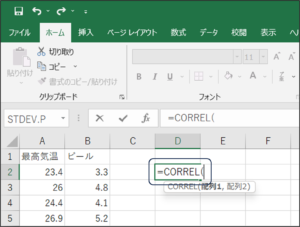
④セルの範囲選択を使用して、最高気温のデータを入力します。
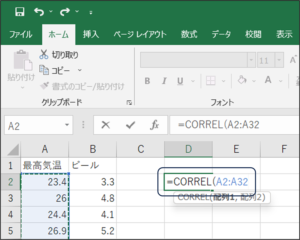
⑤データを区切るため、「,」を入力します。
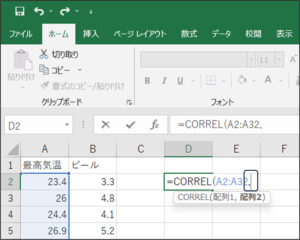
⑥セルの範囲選択を使用して、ビールの売り上げデータを入力し、Enterキーを押します。
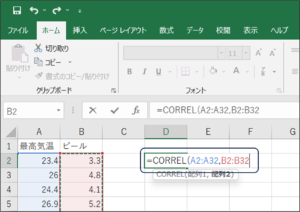
⑦相関分析結果が表示されます。
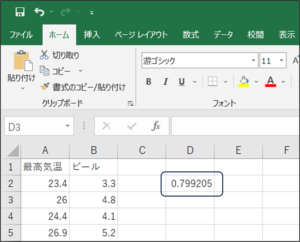
関数を挿入する方法
2つ目の方法は、関数を挿入する方法です。
①セルが選択されている状態で、fxボタンをクリックします。
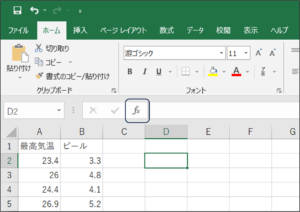
②関数の挿入画面が表示されます。
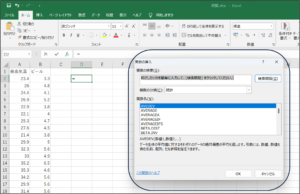
③関数の検索欄に、「相関」と入力し、検索開始(G)ボタンをクリックします。
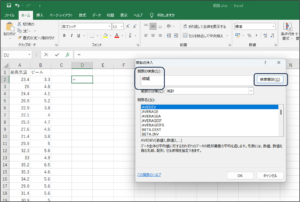
④検索結果の関数名からCORREL関数を選択し、OKボタンをクリックします。
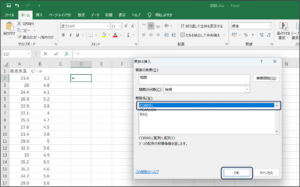
⑤関数の引数画面が表示されます。
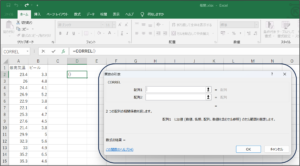
⑥配列1にセルの範囲選択を使用して、最高気温のデータを入力します。
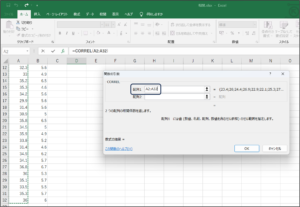
⑦配列2にビールの売り上げデータを入力するため、範囲選択ボタンをクリックします。
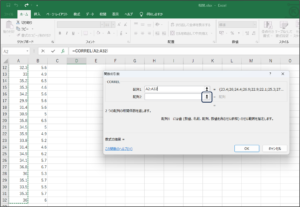
⑧セルの範囲選択を使用して、ビールの売り上げデータを入力後、範囲選択ボタンをクリックします。
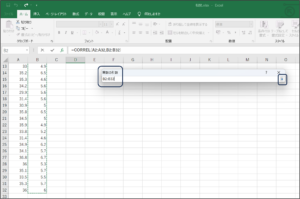
⑨OKボタンをクリックします。
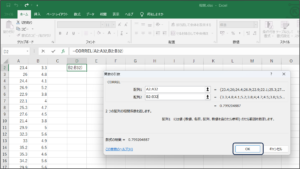
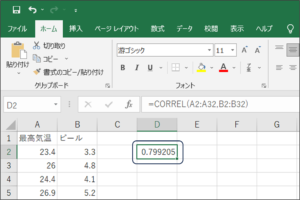
⑩相関分析結果が表示されます。
数式タブから関数を入力する方法
3つ目の方法は、数式タブから関数を入力する方法です。
①セルが選択されている状態で、数式タブのその他の関数の中にある統計のCORREL関数を選択します。
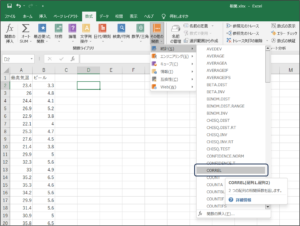
②関数の引数画面が表示されます。
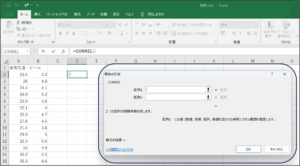
③配列1にセルの範囲選択を使用して、最高気温のデータを入力します。
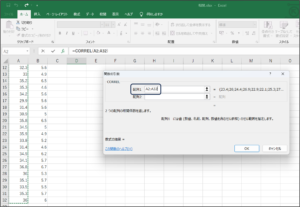
④配列2にビールの売り上げデータを入力するため、範囲選択ボタンをクリックします。
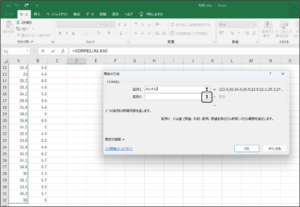
⑤セルの範囲選択を使用して、ビールの売り上げデータを入力し、範囲選択ボタンをクリックします。
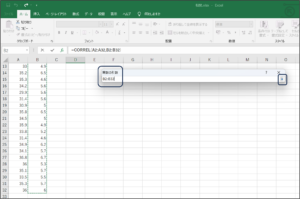
⑥OKボタンをクリックします。
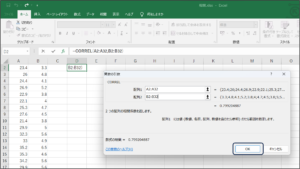
⑦相関分析結果が表示されます。
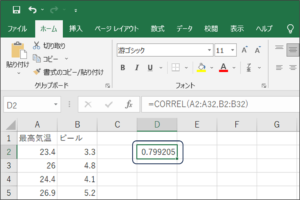
以上の3つの方法で、CORREL関数によるデータ分析を行うことができます。
その他のExcel関数についても、この3つの方法が使用できます。
Excelの分析ツールを使った相関分析の方法
ここからはExcelの分析ツールを使って相関分析を行う方法をご紹介します。
分析ツールの準備
Excelの分析ツールを使用して、相関分析を行います。
分析ツールを使用する前に、Excelの分析ツールが使用できるように設定します。
①Excelを起動し、オプションをクリックします。

②アドインを選択して、管理(A):に「Excel アドイン」を設定し、設定(G) ...ボタンをクリックします。
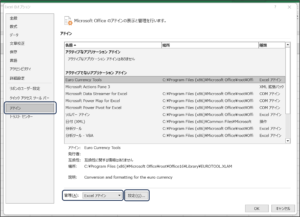
③アドイン画面が表示されますので、分析ツールにチェックをつけ、OKボタンをクリックします。
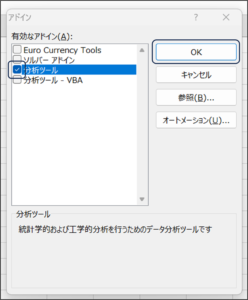
④データタブをクリックし、データ分析が追加されていることを確認します。
データ分析が追加されていれば、データ分析ツールの準備は完了です。

分析ツールを使用した相関分析の方法
Excelの分析ツールを使用した相関分析の方法を説明します。
例として、最高気温とビールの売り上げについての相関分析を行います。
①データタブからデータ分析をクリックします。
②データ分析画面が表示されますので、相関を選択し、OKボタンをクリックします。
③相関の画面が表示されます。
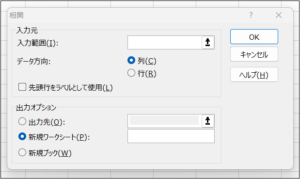
| 項目名 | 説明 |
| 入力範囲(I) | 比較するデータを範囲選択します。 |
| データ方向:列(C) | 比較するデータが列の場合に、チェックを入れます。 |
| データ方向:行(R) | 比較するデータが行の場合に、チェックを入れます。 |
| 先頭行をラベルとして使用(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。
|
| 出力先(O) | 同じシート内に分析結果を出力する場合に、チェックを入れます。 分析結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 分析結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 分析結果を新しいブックに出力する場合に、チェックを入れます。 |
④条件を設定して、OKボタンをクリックします。
⑤相関分析結果が表示されます。
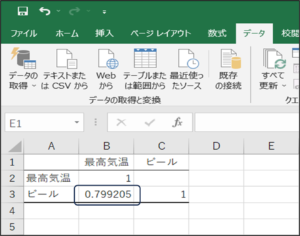
以上で、Excelの分析ツールを使用した説明は終わりです。
相関関係と因果関係の違い
相関があるとしても、必ず因果関係があるとは言えません。
因果関係とは、Aという原因で、Bという結果になるということです。
例えば、ソフトクリームの売り上げとビールの売り上げに強い相関関係があったとします。
しかし、ソフトクリームの売り上げが多ければ、ビールの売り上げも多くなると言えるでしょうか。
ソフトクリームやビールは夏などの気温が高い時に、売り上げが多くなると考えられます。
ソフトクリームの売り上げが多ければ、ビールの売り上げも多くなるのではなく、気温が高い(原因)ため、ソフトクリームとビールの売り上げが多く(結果)なるのです。
ビジネスにおける相関分析の活用事例
相関分析は、マーケティングや社会調査をはじめとする様々な調査の場面で利用される分析です。
「定量データ×定量データ」の2つのデータの間の関連性を見るというのはシンプルな分析ですので、汎用性が高く、多くの場面で活用できる分析手法の一つです。
具体的にどのような場面で利用されるのか、解説していきます。
活用事例① サービス解約者の分析
自社のサービスを解約する人の解約有無情報と、顧客属性情報を利用し相関分析を実施。
そうすることで、どのような人がサービスの解約に至りやすいのか、傾向を発見し、解約防止の施策を考えていく。
活用事例② 販売データの分析
ある商品Aの販売データと購入者の属性を相関分析。
そうすることで、商品Aはどのような人が購入しやすいのか、把握できる。
その結果をもとに、購入しやすい人が集まる地域で精力的に商品Aの販売を決める、など。
活用事例③ コンビニの販売データの分析
コンビニなどで商品を売る場合の商品の配置に活用することができます。
商品ごとの売り上げデータから相関分析を行い、相関関係が強い組み合わせの商品を隣同士に配置しておけば、一緒に購入してもらえる確率が上がり、売り上げアップにつながります。
まとめ
相関分析は、手軽に2種類の定量データ間の関連を見ることができる分析手法として、大変便利です。
ただし、相関係数が高くても一概に関連があるとは言えないという注意点もあります。
データリテラシーを身につけ多角的な視点で正しく活用することで、相関分析はビジネスにも役立つ大変心強い分析になることでしょう。
↓この記事を読んだ方の多くは、以下の記事も読んでいます。