
今回は、統計学のなかでも基本的な度数分布表について解説していきます!
度数分布表は統計検定3級や統計調査士で問われやすいうえ、覚えるとビジネスの場でも役立ちます!
是非この機会に知識を身につけておきましょう!
この記事を読むと分かること
- 度数分布表とは
- 度数分布表の読み取り方
- 度数分布表の作成方法

最後まで楽しんで読んでください!
度数分布表とは
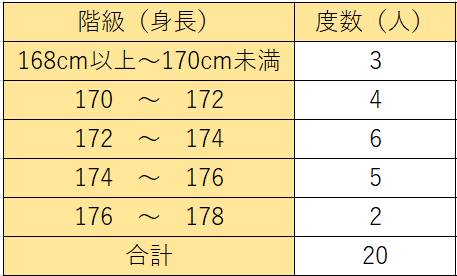
度数分布表とは、データの最小値から最大値までの間をいくつかの階級(グループのようなもの)に分類し、それぞれの階級に含まれる度数を示した表のことです。
具体的には、以下の表が基本的な度数分布表の形です。
また、度数分布表のなかには、
上記の形式に相対度数や累積相対度数などを付け加えた形のものもあります。
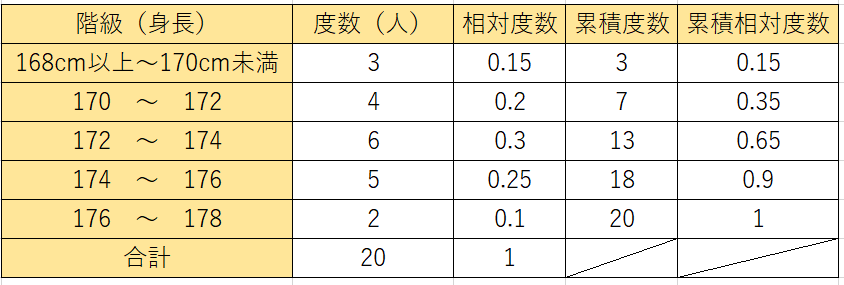
度数分布表で示したい事柄に応じて、適切な形を選びましょう。
度数分布表の読み取り方
度数分布表には、以下のような用語が出てきます。
- 階級・・・データを整理するために用いる区間
- 階級の幅・・・区間の幅
- 階級値・・・階級の真ん中の値
- 相対度数・・・「各階級の度数」÷「度数の合計」
- 累積度数・・・その階級以下の度数を全て合計した値
- 累積相対度数・・・「累積度数」÷「相対度数」or 「その階級以下の相対度数を全て合計した値」
文字でみると、結構ややこしそうですが、実際の度数分布表を見ると意外とシンプルです。
先ほどの表をもう一度出します。
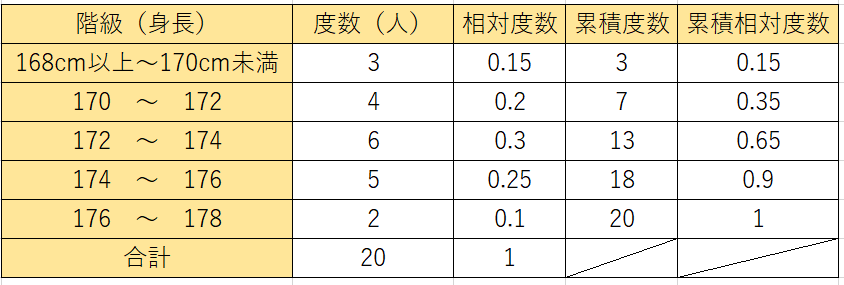
上の表をもとに、先ほどの用語を解説していきます。
| 階級 | 階級のそれぞれの区間。(例:168cm~170cmなど) |
| 階級の幅 | 各階級の最大値から最小値を引いた値。(例:170 - 168 = 2 → 階級の幅は2cm) |
| 階級値 | 階級の真ん中の値。各階級の最大値と最小の平均を求めればよい。 |
| 相対度数 | 「各階級の度数」を「度数の合計」で割った値 |
| 累積度数 | その階級以下の度数を全て合計した値 |
| 累積相対度数 | その階級以下の相対度数を全て合計した値 |
度数分布表の作成方法
度数分布表の作成には、以下のような3つの手順があります。
度数分布表作成手順
- 階級の幅を設定する。
- 分布表における階級の最小値を設定する。
- 数え上げて度数を表に記入していく。
階級の幅を設定する。
階級の幅は自由に設定できますが、幅が狭すぎると階級が多くなりすぎたり、逆に幅が広すぎると階級が少なすぎて、度数分布表からデータの特徴をつかみにくくなります。
データの特徴を読み取りやすくなるような、
適度な階級の数、階級の幅を設定していきましょう。
ちなみに、階級幅は、必ずしも全ての階級が等間隔にする必要はありません。
例えば、所得の度数分布表を作成する場合は、高所得者が少ないため、低所得者と同じ階級幅比すると、十分なデータが集められない可能性があります。
そのため、そのような場合、一般的には高所得者の階級の幅を広くとります。
データに合わせて適切な階級幅を設定することが大切ということですね。
分布表における階級の最小値を設定する。
例えば、所得の度数分布表を作成するからと言って、必ず0円から表を作らなければいけないわけではありません。
一般的な正社員の所得を分析する場合に、わざわざ0~50万円などの階級まで載せたりすると、データも少ないうえ、あまり重要なところじゃないのに、度数分布表の階級が多くなるため見にくくなってしまいます。
そのため、200万円~の階級から度数分布表を作成する、といったように
自分の分析に適した、分布表における階級の最小値を設定する必要があります。
数え上げて度数を表に記入していく。
上記の条件を設定したら、あとはその条件に沿って地道に数えて、度数分布表に記入していくだけです。
間違えないように、それぞれの度数を足したら合計と一致するか、相対度数を全て足したらちゃんと1になるかなどを確認する癖をつけておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





