研究やお仕事の中でデータ解析をする時、「主成分分析」という手法を聞いたたことがある方もいらっしゃるかもしれません。
主成分分析とは、変数が多く、複雑なデータを分かりやすく要約するための手法です。
多くの要因を考える必要があるビッグデータの解析にも力を発揮する手法です。
しかし、難しい用語が多く、回帰分析などの手法と比べると結果も解釈しづらいため、使うのをためらっている方も多いのではないでしょうか。
そこで、本記事では主成分分析の特徴や結果の見方を分かりやすく説明します。
主成分分析の特徴
主成分分析できること~情報の要約~
主成分分析とは、変数の数を減らし、データを解釈しやすくするための手法です。
昨今、様々な話題になっているビッグデータも、変数の数が多すぎて、人間が傾向を掴むのは難しいことが多いです。
例えば、商品の売り上げ一つとっても、その日の天気や気温、駅からの距離、など様々な変数が影響しています。
こういった変数から傾向を掴めれば売り上げの改善策を提案できるかもしれません。
ですが、変数が多すぎるため、そのままでは可視化したり重回帰分析などの解析を行ったりするのも困難です。
このようなデータについて主成分分析を使うと、より少ない変数で表現でき、グラフ化や解析がしやすくなることがあります。
(引用元:https://gmo-research.jp/research-column/principal-component-analysis)
「変数を減らす」とはどういうことでしょうか?
身近な事例として、BMIを例に挙げて考えてみましょう。
BMIとは、Body Mass Indexという指標であり、「(体重(kg))/(身長(m))2」という式で計算されます。
ご存じの方も多いとは思いますが、BMIは肥満度の指標として用いられます。
つまり、「体重」・「身長」を、「肥満度」という指標に落とし込んだ、つまり変数の数を減らしたといえます。
なお、このように変数を減らすことを「次元削減」と呼ぶこともあります。
主成分分析の具体例
テストの結果を分析する事例を用いて、主成分分析のイメージを掴んでいただきます。下表のようなテストの結果があったとします。
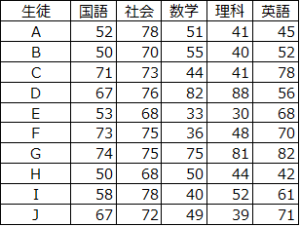
この表を見ても、全体の傾向は掴みづらいのではないでしょうか。
「Eさんは文系寄りなのかな?」という大まかな傾向は分かるかもしれませんが、他の生徒と比較したときの結果などは分からないでしょう。
また、5科目なので、グラフ化することもできません。
しかし、主成分分析をするとより多くの情報を得ることができます。
具体的には、次のようなことが分かります。
・各生徒の総合的な学力が比較できる
・各生徒が文系・理系どちらに寄っているか分かる
さらに、グラフ化することにより各生徒の能力分布を把握できます。「主成分得点」という言葉の意味は後述します。

なお、横軸の「第1主成分」というものは総合学力を示し、縦軸の「第2主成分」は各生徒の能力が理系寄りか文系寄りかを示しています。
第2主成分がプラスだと文系寄り、マイナスだと理系寄りという解釈ができます。
(計算には「mam相関分析・主成分分析~(無料)フリーソフト」を使用 データも同梱のサンプルデータを使用)
主成分分析の分析方法
結果の見方
テストの点数に対して主成分分析を行った事例を通し、結果の見方を説明します。
計算自体は各種統計分析ソフトで可能です。
固有値と寄与率
この項目は、どの主成分まで考えるべきかという情報を与えてくれます。

詳細な説明は省きますが、固有値が大きいほどその主成分がデータの説明によく貢献していると考えて差し支えないです。
明確な基準はありませんが、固有値が1を超えている主成分を採用するとよいでしょう。
寄与率は、各主成分がデータ全体をどのくらいの割合で説明できているか表します。
この場合は、第2主成分までで全体の8割程度を説明できているといえます。
今回は第1、第2主成分のみを考えれば全体の傾向をおおよそ理解できるといえるでしょう。
主成分負荷量
この指標は、各主成分に対してどの変数の寄与が大きいかを示しています。
これを見ると、各主成分の意味合いを読み取ることができます。
今回は第2主成分までを考えます。

第1主成分の主成分負荷量を見ると、どの科目に対してもすべてマイナスであることが分かります。
どの科目も、第1主成分には同じように寄与しています。
つまり、第1主成分はすべての科目に共通する基礎学力のようなものを示していると解釈できます。
点数が増えるほど第1主成分が小さくなることから、第1主成分が小さいほど基礎学力が高いと読み取れます。
第2主成分を見ると、国語、英語では大きくプラスの値になっており、数学、理科では大きくマイナスの値をとっています。
つまり、文系科目ではプラス、理系科目ではマイナスになるという傾向があるといえます。
つまり、第2主成分は文系と理系の能力を分けるような指標だと推測できます。
主成分得点
元のデータを各主成分の値に変換したものです。
これを用いると、各生徒の総合能力、文系・理系能力の傾向を把握できます。
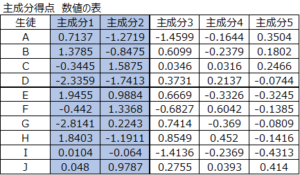
このデータから散布図を作り、可視化すると下のようになります。
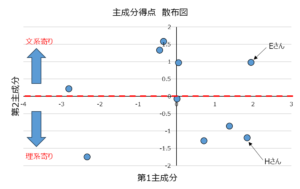
これを見ると、EさんとHさんの第1主成分得点は同程度であるため、総合的な学力は同程度と解釈できます。
しかし、第2主成分得点はプラスとマイナスがほぼ逆のようになっており、どちらかというとEさんは文系寄り、Hさんは理系寄りということが分かります。
主成分分析により、5科目のテスト結果の傾向を2変数の散布図で大まかに表すことができるようになりました。
注意点
注意点として挙げられるのは、主成分の意味分析者が考えなければならないということです。
今回の例では、各科目の主成分負荷量を比較し、「第2主成分は文系・理系能力を表す」ということに気づくことができました。
あくまで主観的な結果であるため、可能であれば他の人と相談し、慎重に主成分の意味を考えるようにしましょう。
まとめ
主成分分析でできることや、結果の見方を説明しました。
主成分分析は、データの可読性を向上させるための手法です。
ビッグデータなど、変数が多すぎて解釈に苦労するようなデータを扱う際に非常に有効な手法です。
アンケート調査や各種ランキングに用いられる指標作成など、私たちの身の回りでもよく使われています。
この記事を読んでいる方のも、データを分析する中で主成分分析を使う場面が来るかもしれません。
その時は、本記事を参考に主成分分析について理解を深めていただければ幸いです。
(参考サイト)
https://www.nttcoms.com/service/research/dataanalysis/principal-component-analysis/
https://www.statweb.jp/method/tahenryo-kaiseki/syuseibun-case







