いきなりですが、皆さんは単回帰分析という分析方法をご存じでしょうか。
Excelでも簡単にできて非常に便利な分析方法なのですが、統計学を学んでいない方ですとなかなかご存じでない方が多一かもしれません。
今回は、そんな回帰分析の中でも最も基本的な分析方法である「単回帰分析」について解説していきたいと思います!
覚えればビジネスの現場でもすぐに使えるようなすごく便利な分析方法なので、是非最後まで読んでみてください!
この記事を読むと分かること
- 単回帰分析ってなに?
- Excelで単回帰分析をする方法
- 出力結果の読み取り方
回帰分析とは
近年、ビッグデータの活用といった「データを分析して将来を予測する」ということがトレンドになっています。
この将来を予測するための分析の1つが「回帰分析」です。
単回帰分析は、結果に影響を与える要因となる変数が1つであり、その1つの変数から結果を予測する方法です。
要因となる変数は「説明変数」や「独立変数」と呼ばれ、結果にあたる変数は「目的変数」などと呼ばれます。
例えば、全国の高校生の身長と体重のデータを使って、身長から体重を予測したい!という場合には、身長が「説明変数」、体重が「目的変数」となります。
単回帰分析の場合は、説明変数をx、目的変数をyとした時に、y = ax + bで表される式によって結果を予測していきます。
aとbには「回帰係数」と呼ばれる1つの値が入り、xにある値を入れると自動的にyの値が求まるようになっています。
先ほどの身長から体重を予測する際に、回帰分析を行った結果「y = 0.6x – 40」という式が求められたとします。
ある1人の生徒の身長が164cmだった時の体重を予測する際には、この式のxに164を代入することで、その生徒の体重がy=0.6×164 – 40=58.4[kg]であると予測されます。
相関分析との関係
先ほどの式を見て気づいた方もいるかもしれませんが、単回帰分析の一般式は、直線の式になっています。 aにあたる部分が直線の傾きで、bにあたる部分が切片になっていますね。
なぜ単回帰分析の一般式は、直線の式で表すことができるのでしょうか。
そこには相関が大きく関係しています!
相関分析は、2つの変数間にどの程度の関連があるのかを見る分析方法ですが、あくまで関連の強さを見ているだけなので、ある変数の値から別の変数の結果を予測することはできません。

上の図のように、散布図に直線を当てはめることで、2つの変数に関連があるのでは?というざっくりとした判断だけではなく、具体的な数値で変数間の関係を表すことができるようになります。
その結果、原因から結果を予測することができるようになるというのが単回帰分析です。
関連が見られそうなデータに直線を当てはめることで、結果を予測する手法だということは単回帰分析のポイントの1つです!
Excelを使った単回帰分析の具体的な手順
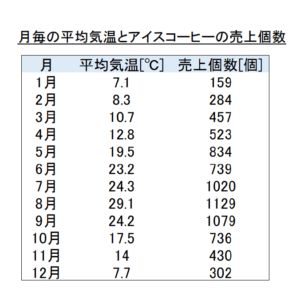
今回は、あるカフェのアイスコーヒーの売上個数と気温に関する仮想データを使って、実際に回帰分析を行ってみたいと思います!
まず、以下のような月ごとの平均気温とアイスコーヒーの売上個数のデータがあったとしましょう。
今回は、Excelを用いた回帰分析の手順を紹介します。
出力された結果をどのように見れば良いのかについても説明していくので、この記事を読みながら実際にExcelを動かしてみてください!
まずはデータの相関を見てみる
回帰分析を行う前に、まずはデータにどのような関連がありそうかx軸に平均気温、y軸にアイスコーヒーの売上個数を取った散布図を作成してみたいと思います。
Excelで散布図を作成するには、散布図を作成したいデータの範囲を選択し、「挿入→グラフ散布図」をクリックします。
軸やグラフのタイトルなど、細かい部分の体裁を整える必要はありますが、今回はそのまま進めていきます。 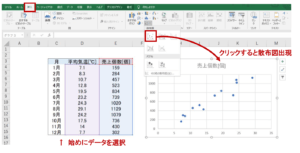
散布図を見ると、気温が上がるとアイスコーヒーの売上個数も上昇するという右肩上がりの傾向にありそうですね。
ここから、アイスコーヒーの売上個数には気温が影響しているのではないか?という仮説が立てられます。
散布図に直線の式を当てはめる
散布図に直線の式を当てはめて、右肩上がりの傾向を具体的な数値で示してみましょう。
Excelで散布図に直線の式を当てはめる方法はとても簡単です!
先ほど作成した散布図をクリックして、右上の+で書かれている「グラフ要素」のボタンを押します。
一番下に「近似直線」という選択肢があるので、チェックマークを付けると散布図から導かれる近似直線が引かれます。 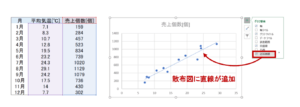
先ほど紹介した回帰分析の一般式を出す場合には、「グラフ要素→その他のオプション→グラフに数式を表示する」のチェックボックスにチェックを付けると数式が出てきます。
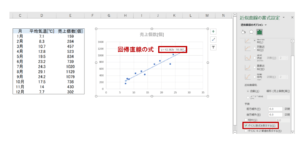
今回の散布図から求められる回帰直線はy=42.362x-59.387という式で表されるので、気温が27℃だった場合には、x=27を代入してy=42.362×27-59.387=1084.387となり、アイスコーヒーは約1084個売れると予測されます。
分析ツールで当てはまりの良さを評価する
ところで、回帰係数の42.362という値や59.387という値は本当に正しい値と言えるのでしょうか。
回帰直線の当てはまりの良さや、本当に影響を与える変数によって予測をしているのかどうかを調べるために、Excelの分析ツールを用いて細かく分析していきたいと思います!
分析ツールはデータの右端に表示されているものですが、もし表示されていない場合には「ファイル→オプション→アドイン」の設定から分析ツールにチャックを入れてOKボタンを押すことで表示されるようになります。 
分析ツールが表示されれば、あとは分析に用いる数値の範囲を入力していくだけです!
「データ→データ分析→回帰分析」の順に進んでいき、数値の範囲をドラッグすることで「入力先」に値の範囲を入力してOKを押します。
有意水準など細かい設定もありますが、今回はデフォルトの有意水準5%での検定を行った結果を出力します。 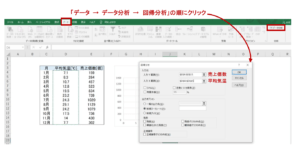
入力先には「X範囲」と「Y範囲」がありますが、X範囲が説明変数のデータの範囲、Y範囲が目的変数のデータの範囲にあたるので、今回の例ではX範囲に平均気温、Y範囲に売上個数のデータの範囲を指定します。
出力結果の読み取り方
分析ツールで回帰分析を行った結果は、別のExcelシートにこのように出力されます。 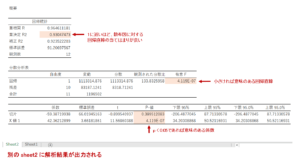
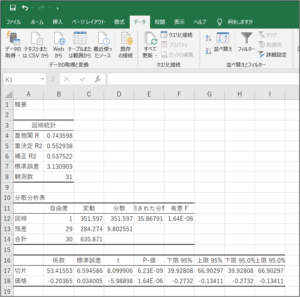
出力された結果は数字が並んでいて、解釈するのが難しそうですが、まずは「重決定R2」と「有意F」、「p値」を見ると良いと思います。
「重決定R2」は決定係数と呼ばれ、回帰直線全体の当てはまりの良さを表しています。
決定係数は0から1までの範囲を取り、1に近いほど回帰直線の当てはまりが良いことを示しています。
今回の例では決定係数が0.9を超えているので、散布図から引いた直線の当てはまりが非常良いことを示しています。
「有意F」は意味のある回帰直線が引けているかどうかを表しています。
有意Fの値が小さければ、結果に影響のある変数を用いた回帰直線が引けていると言うことができます。
最後に「p値」です。 ここでのp値は、それぞれの回帰係数が意味のある値かどうかを表しています。
P値が0.05以下であれば意味のある回帰係数であることを示しています。
重回帰分析とは
重回帰分析を一言で表すと、原因とみられる複数の要素が結果にどの程度影響を与えているのかを数値化し、複数の要素から結果を予測できるようにする分析手法のことです。

一言で表すとなんだか堅苦しい印象を受けますが、分析の流れや仕組みは単回帰分析とほとんど同じです。
単回帰分析についても少しおさらいしながら、単回帰分析と重回帰分析の違いや重回帰分析の特徴について見ていきましょう!
単回帰分析との違い
単回帰分析は、原因とみられる1つの要素からある結果を予測するための手法でした。
原因にあたる変数は「説明変数」と呼ばれ、結果にあたる部分は「目的変数」と呼ばれています。

単回帰分析で結果を予測する際には「y=ax+b」という直線の式を用いて、xの部分に説明変数の値を代入することで、yの目的変数の値を予測していくという流れでしたね。
重回帰分析でも、さきほど出てきたような「説明変数」「目的変数」という用語は同じように使います。
原因から結果を予測するという分析の根底にある目的も同じです。
しかし、重回帰分析は「説明変数が複数存在している場面」で結果を予測する場合に用いる手法なので、結果を予測する際に用いる式が単回帰分析と異なります。
重回帰分析で結果を予測するために用いる「回帰式」は以下のようになります。
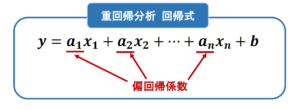
aやbで表されている部分は「偏回帰係数」と呼ばれます。
重回帰分析のメリット
重回帰分析では、原因とみられる複数の変数から結果を予測するというのが一番大きな目的です。
そして、複数の変数を用いて結果を予測しているので、それぞれの変数が結果にどの程度の影響を与えているのか、影響の大きさを比較することができるという点が、重回帰分析の大きなメリットです。
先ほど紹介した回帰式の中にある偏回帰係数は、温度や個数などそれぞれの変数で単位が異なるので、結果への影響をそのまま比較することはできません。
しかし、そこで変数を標準化した「標準化偏回帰係数」というものを算出することで、どの変数が結果に大きく影響を与えているのかを比較することができるようになります!
これは単回帰分析にはできない、重回帰分析ならではの特徴です。
重回帰分析の出力結果の読み取り
それでは、Excelを用いて実際に重回帰分析を行ってみましょう。 今回は、飲食店の年間売り上げに影響を与えている複数の要因から、新店舗の売り上げを予測してみたいと思います。
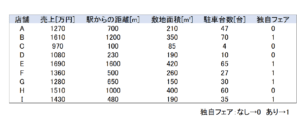
上のデータのように、各店舗の売り上げには駅からの距離、敷地面積、駐車台数、店舗ごとに独自のフェアを行っているかどうかが関係しているのではないかと考えたとします。
駅からの距離、敷地面積、駐車台数、店舗独自のフェア実施の有無を説明変数、年間売り上げを目的変数として重回帰分析を行います。
ここで注意点があります。
今回の例のような「店舗独自のフェアの有無」は通常「あり」「なし」などの2つの選択肢で表されます。
しかし重回帰分析を行う場合は、これを数値に置き換える必要があります。
回帰分析はそれぞれの要素の影響を数値で表すことが目的なので、「あり」を1、「なし」を0といった数値に置き換える作業を行ったうえで分析を進めていきます。
出力結果の読み取り方
Excelでの回帰分析の実施方法は「単回帰分析とは Excelでの求め方や活用事例とともに解説」で詳しく紹介しているので、ここでは分析の流れについての説明は割愛します。
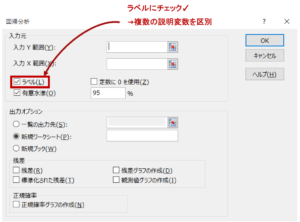
一点注意点として、重回帰分析は説明変数が複数あります。 そのため、分析ツールを開いた時に「ラベル」にチェックを入れるのを忘れないようにしてください。
今回は分析の流れよりも、出力された重回帰分析の結果をどのように解釈していけば良いかに焦点を当てていきたいと思います。
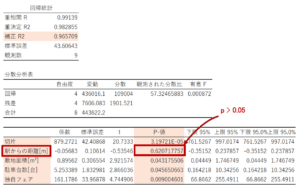
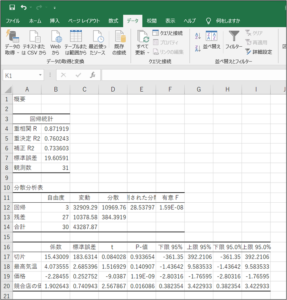
重回帰分析を行った結果、上のような表が出力されました。
ぱっと見では単回帰分析と同じような結果が出力されていると思いますが、一番下の表に複数の説明変数に対する結果が出力されているのが分かるかと思います。
結果の見方についてですが、重回帰分析の場合には「自由度調整済み決定係数」と呼ばれる「補正R2」の値を見て、上手く説明が出来ているかを判断すると良いと思います。
「補正R2」も「重決定R2」と同様に、1に近づくほど上手く説明が出来ていることを表しているので、今回の重回帰分析で求められた式を用いれば、新店舗の売り上げも上手く予測できることを表しています。
また一番下の表は、それぞれの説明変数がどれほど結果に寄与しているのか、本当に結果に影響を与えられる変数なのかを検討した結果となっています。
この結果から、新店舗の年間売り上げを予測する際にはこのような式を用いれば良いということが分かります。
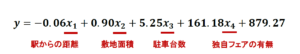
例えば新店舗をオープンさせたい場所が、駅から700m、敷地面積が350m²、駐車台数は20台だった時に、店長の意向で独自のフェアを実施する場合には年間約1257万円の売り上げ、独自フェアを行わない場合には年間約1418万円の売り上げが見込める、ということが分かります。

一番下の表に出力されているP値は、それぞれの変数が結果に影響を与えることができる意味のある変数かどうかを表しています。
p値が0.05を下回っていれば意味のある変数だと言えますが、今回の場合は駅からの距離に対するp値が0.05を上回っているので、回帰式に強く影響を与える変数ではない可能性があります。
このような場合には、駅からの距離を除いて再び重回帰分析を行ってみると、より精度の良い回帰式が出来上がる場合があります。
Excelを使って回帰分析を行う方法
回帰分析を行う方法として、散布図から近似曲線と決定係数を導き出す方法と分析ツールを使う方法があります。
散布図から近似曲線と決定係数を導き出す
最初に、散布図から近似曲線と決定係数を導き出す方法を説明します。
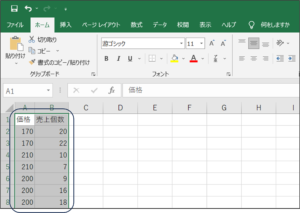
例として、価格(原因)と売上個数(結果)の回帰分析を行います。
①セルの範囲選択を使用して、価格と売上個数のすべてのデータを選択します。
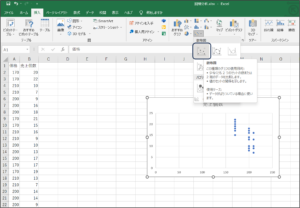
②挿入タブの「散布図(X,Y)またはバブルチャートの挿入」の「散布図」をクリックします。
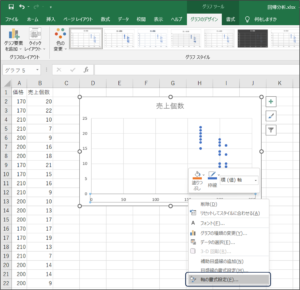
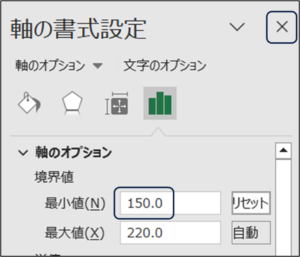
③散布図を見やすくするため、横軸の数字を左クリックして、横軸が囲まれたら、右クリックし、「軸の書式設定(F)...」をクリックします。
④軸の始まりを示す境界値の最小値(N)が「0」になっていますので、「150.0」に変更し、Enterキーを押し、×をクリックし、画面を閉じます。
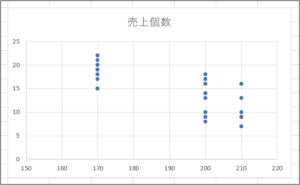
⑤横軸が「150」から始まり、散布図が見やすくなります。
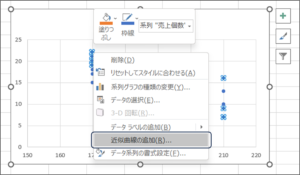
⑥散布図の点を選択して、右クリックし、「近似曲線の追加(R)...」をクリックします。
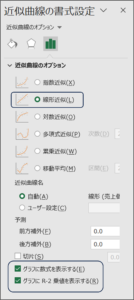
⑦「線形近似(L)」、「グラフに数式を表示する(E)」、「グラフにR-2乗値を表示する(R)」にチェックを入れて、×をクリックし、画面を閉じます。
⑧分析結果として、近似曲線と決定係数が表示されます。

Excelの分析ツールを使用して、回帰分析を行う方法
Excelの分析ツールを使用して、回帰分析を行います。
分析ツールの設定
分析ツールを使用する前に、Excelの分析ツールが使用できるように設定します。
①Excelを起動し、オプションをクリックします。

②アドインを選択して、管理(A):に「Excel アドイン」を設定し、設定(G) ...ボタンをクリックします。 
③アドイン画面が表示されますので、分析ツールにチェックをつけ、OKボタンをクリックします。

④データタブをクリックし、データ分析が追加されていることを確認します。
データ分析が追加されていれば、データ分析ツールの準備は完了です。

Excelの分析ツールを使用した回帰分析の方法
Excelの分析ツールを使用した回帰分析の方法を説明します。
単回帰分析の場合
例として、価格(原因)と売上個数(結果)の回帰分析を行います。
①データタブからデータ分析をクリックします。
②データ分析画面が表示されますので、回帰分析を選択し、OKボタンをクリックします。
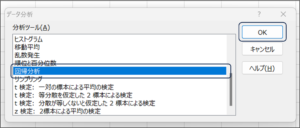
③回帰分析画面が表示されます。
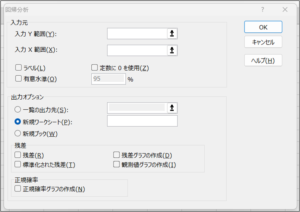
| 項目名 | 説明 |
| 入力Y範囲(Y) | 結果となるデータを範囲選択します。 |
| 入力X範囲(X) | 原因となるデータを範囲選択します。 |
| ラベル(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。 |
| 定数に0を使用(Z) | 切片が「0」の場合に、チェックを入れます。 |
| 有意水準(O) | 信頼区間の比率を設定します。 結果は、初期値である95%信頼区間とここで設定した信頼区間の比率の結果の2種類が出力されます。 |
| 一覧の出力先(S) | 同じシート内に分析結果を出力する場合に、チェックを入れます。 分析結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 分析結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 分析結果を新しいブックに出力する場合に、チェックを入れます。 |
| 残差(R) | 結果と予測値の差を出力する場合に、チェックを入れます。 |
| 残差グラフの作成(D) | 残差に加え、残差のグラフを出力する場合に、チェックを入れます。 |
| 標準化された残差(T) | 残差に加え、標準残差を出力する場合に、チェックを入れます。 |
| 観測値グラフの作成(I) | 結果と予測値のグラフを出力する場合に、チェックを入れます。 |
| 正規確率グラフの作成(N) | 正規確率グラフを出力する場合に、チェックを入れます。 |
④入力Y範囲にセルの範囲選択を使用して、結果である売上個数のデータを入力します。
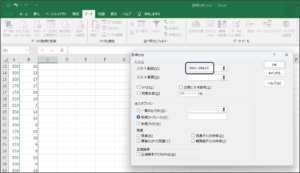
⑤入力X範囲に原因である価格を入力するため、範囲選択ボタンをクリックします。
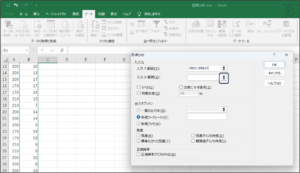
⑥セルの範囲選択を使用して、価格データを入力後、範囲選択ボタンをクリックします。 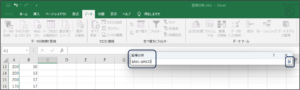
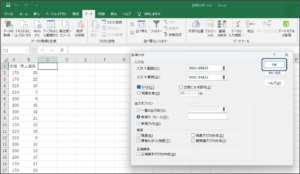
⑦その他の条件を設定し、OKボタンをクリックします。
⑧回帰分析結果が表示されます。
重回帰分析の場合
最後に、複数の原因が考えられる場合に結果との関係を分析する重回帰分析を説明します。
例として、最高気温(原因)、価格(原因)、競合店の価格(原因)と売上個数(結果)の重回帰分析を行います。
①データタブからデータ分析をクリックします。
②データ分析画面が表示されますので、回帰分析を選択し、OKボタンをクリックします。
③回帰分析画面が表示されます。
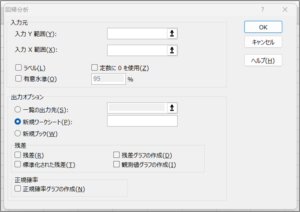
| 項目名 | 説明 |
| 入力Y範囲(Y) | 結果となるデータを範囲選択します。 |
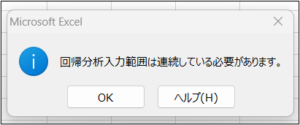
| 入力X範囲(X) | 原因となるデータを範囲選択します。 重回帰分析の場合に、原因となるデータの範囲選択が連続していない場合は、以下のエラーメッセージが表示されます。 ※今回のデータであれば、最高気温と競合店の価格を範囲指定した場合 |
| ラベル(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。 |
| 定数に0を使用(Z) | 切片が「0」の場合に、チェックを入れます。 |
| 有意水準(O) | 信頼区間の比率を設定します。 結果は、初期値である95%信頼区間とここで設定した信頼区間の比率の結果の2種類が出力されます。 |
| 一覧の出力先(S) | 同じシート内に分析結果を出力する場合に、チェックを入れます。 分析結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 分析結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 分析結果を新しいブックに出力する場合に、チェックを入れます。 |
| 残差(R) | 結果と予測値の差を出力する場合に、チェックを入れます。 |
| 残差グラフの作成(D) | 残差に加え、残差のグラフを出力する場合に、チェックを入れます。 |
| 標準化された残差(T) | 残差に加え、標準残差を出力する場合に、チェックを入れます。 |
| 観測値グラフの作成(I) | 結果と予測値のグラフを出力する場合に、チェックを入れます。 |
| 正規確率グラフの作成(N) | 正規確率グラフを出力する場合に、チェックを入れます。 |
④入力Y範囲にセルの範囲選択を使用して、結果である売上個数のデータを入力します。
⑤入力X範囲に原因である最高気温、価格、競合店の価格を入力するため、範囲選択ボタンをクリックします。
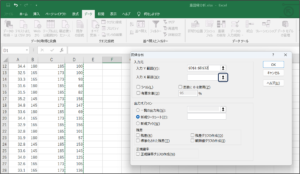
⑥セルの範囲選択を使用して、最高気温、価格、競合店の価格データを入力後、範囲選択ボタンをクリックします。

⑦その他の条件を設定し、OKボタンをクリックします。
⑧重回帰分析結果が表示されます。
ビジネスにおける回帰分析の活用事例
たとえば、回帰分析で回帰式を求めれば、気温が35度なら今日はアイスが100本程度売れるだろうといったような売上予測ができます。
また、顧客満足度の調査から、価格や接客態度など、どの項目を改善すれば、顧客満足度がアップするかという影響度がわかります。
ほかにも、身長と体重の関係を調査し新薬の開発に役立てる、ある商品に費やした広告費が売上に影響しているか、年齢がある薬の効果に影響を与えているのかなど、非常に幅広い場面で活用できます。
例えば、ある薬の効果は年齢だけではなく、性別、肥満度、元々持っている疾患の有無とも関連している可能性がある場合には、単回帰分析よりも重回帰分析を行った方が予測の精度が上昇します。

また、飲食店の新店舗の売り上げを予測したいと考えている時に、系列店の売り上げに影響を与えている要因から予測をする場合には、店舗の広さや駅からの距離など様々な要因が売り上げに影響を与えていると考えるのが妥当です。
科学の分野でもマーケティングの分野でも、たった1つのことが原因で物事が起きていると考えられる場面は少ないと思います。
だからこそ、重回帰分析は単回帰分析よりも使い勝手の良い分析方法だといえるでしょう。
まとめ
今回は回帰分析について、詳しく解説していきました。
回帰分析自体はとても奥が深い分析手法です。
「関連がありそうなデータに対して原因から結果を予測する手法である」という基本を忘れずに勉強を進めていきましょう!
この記事を読んだ方にオススメの記事はこちら!