
こんにちは、統計ブロガーのにっしーです!
いきなりですが、統計学を学ぶ上でとても重要な2つの概念として「統計的推定」と「統計的仮説検定」があります。
ただ、初心者や独学の方がつまずきやすいポイントでもあります。
そこで今回は、初心者の方でもわかるように、統計的仮説検定がどのように活用されるのかをなるべく分かりやすく解説していきます。
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- 統計学でよく聞く仮説検定ってなに?
- 検定と推定の違いって?
- 仮説検定の種類

是非最後まで楽しんで読んでいただければ幸いです!
仮説検定とは?
仮説検定とは、母集団に関する仮説を立てて、その仮説が正しいかどうかを標本のデータから確率的に検証して判断する手法をいいます。
「仮説を立てる」というと難しいことのように聞こえますが、後ほど身近な例を用いて仮説検定を実際に行ってみたいと思いますのでご安心ください。
まずは、仮説検定がどのようなことを指すのか、大まかな概念を理解しましょう!
「推定」と「検定」の違い
冒頭で、統計学を学ぶ上で重要な2つの概念が「統計的推定」と「統計的仮説検定」だというお話をしました。
推定と検定は名前も似ていますし、母集団や標本といったキーワードが共通しているので、「どう違うの?」と思う方もいるかと思います。
推定と検定にはいったいどのような違いがあるのでしょうか。
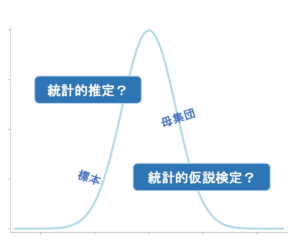
推定と検定の最も大きな違いは、明らかにしたいことや最終的な結論が違うということです。
推定は、母集団の平均や分散といった真値がどのあたりにあるのかを明らかにするために、真値はある1点、または一定の範囲にあるということを推測するものです。
1つの値や上限と下限を求めた信頼区間を求めることで推測しているので、最終的な結論は何かの判定や良し悪しではありません。
一方で、検定は母集団の平均値など、こうなのではないか?と考えた仮説が、本当に正しいと言えるのかを判断するためのもので、最終的な結論は有意差があるかないかとなります。
どちらも標本の平均や標準偏差などの同じ情報を使ってはいますが、実は目的も結論も違うので、推定と検定は全く異なる手法であるということは覚えておいてください!
仮説検定の種類はさまざま
仮説検定の概念についてはお話しましたが、実は仮説検定にはたくさんの種類があります。
よく用いられる検定には以下のようなものがありますが、基本的なものだけでもたくさんの種類があって、見慣れない言葉も多いですよね。

ここでは、それぞれの検定の手法について理解する必要はありませんが、明らかにしたいことや既に分かっている情報が異なれば検定の種類も変わるということだけ覚えておいてください。
仮説検定の手順
まずは、仮説検定の手順についてざっくりと紹介していきます。
仮説検定の具体的な手順は以下の通りです。
仮説検定の手順
- 検証したい仮説を設定する
- 検証したい仮説とは逆の仮説を「帰無仮説」とする
- 検定統計量を求める
- 有意水準と比較して有意差の有無を判定する
この大まかな流れだけでは、検定統計量と呼ばれる値はどのように計算しているのかなどわかりづらい部分も多いと思います。
ここからは実際に身近な例を用いて計算しながら、先ほどの仮説検定の流れに沿って解説していこうと思います。
仮説検定の事例
今回は、新型コロナウイルスの影響による販売休止が相次いでいるフライドポテトを例にして仮説検定を行ってみたいと思います。
あるハンバーガー店では、フライドポテトは平均80g、標準偏差4gとなるように規定しています。
このフライドポテトの重さが本当に80gとなっているのかを確認するために、ランダムに取り出した9個のフライドポテトの重さを計測してみたところ、以下の表の通りであることが分かりました。

この結果から、「フライドポテトの重さは80gからずれている」という仮説を立てて、有意水準を5%とした検定を行いたいと思います。
この時点で、➀の検証したい仮説の設定ができました。
仮説の設定が出来たので、➁にあたる帰無仮説は「母集団の平均は80gである」になります。
今回は、フライドポテトの重さが正規分布に従うことを仮定しますが、正規分布に従っており、母集団の分散が既に分かっている場合には、Z検定を行うことになります。
これらの情報をもとに、➂の検定統計量を計算していきます。
検定統計量を求める
Z検定の検定統計量は、以下の式で求めることができます。
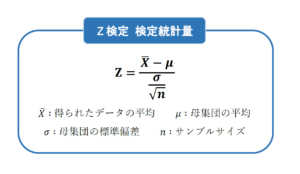
Z検定の検定統計量は、「標準化」とよばれる変換を行うことで求められる検定統計量です。
平均や標準偏差がさまざまな正規分布それぞれについて、ある範囲に入る確率を求めていこうとすると、難しい積分の計算が必要になるのでとても面倒です。
そこで、一度平均0、標準偏差1の標準正規分布に変換する検定統計量を求めることで、有意水準との比較が圧倒的にしやすくなります!
今回の例では、母集団の平均が80、標準偏差が4であり、サンプルサイズが9であるフライドポテトの重さから得られたデータの平均は82.67となっています。
これらの情報を上の式に当てはめてZ統計量を求めると、このようになります。
Z=(82.67-80)/(4/√9)=2.67/1.334=2.001
Z統計量を求めることができれば、あとは有意水準との比較をして有意差があるかどうかについて判定をするだけです!
有意差を判定する
ここで一度、今回の仮説検定の目的や分かっている情報をおさらいします。
今回はフライドポテトの重さが規定の80gからずれているということを明らかにしたいと考えています。
母集団の平均は80、標準偏差は4としており、有意水準5%のZ検定を行います。
ここで、得られたデータの平均が母集団の平均よりも大きい、あるいは小さいことを明らかにしたい場合には、「両側検定」を行います。
「片側検定」というパターンもありますが、今回は両側検定のみ紹介したいと思います。
有意水準5%の両側検定を行う時には、「1.96」という数字がポイントとなります!
正規分布についての解説記事でも紹介しましたが、これは標準正規分布の平均から左右に標準偏差1.96個分の範囲が、全体の95%を占めるという所から来ています。
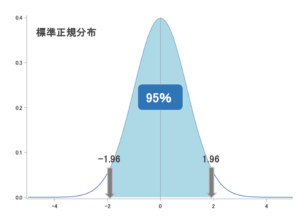
この1.96という数字を用いて、検定統計量が1.96よりも大きい場合、あるいは-1.96よりも小さい場合には、設定した範囲よりもずれが大きいとして「有意差あり」と判定します。
今回の場合であれば、検定統計量Z=2.001なので1.96よりも大きい値となっていますね。
ですので、「母集団の平均は80gである」という帰無仮説は棄却され、フライドポテトの重さは80gからずれているという結論になります。
少し難しい部分もあったかもしれませんが、既に分かっている情報とデータから求められる情報から仮説が正しいかどうかを判定していくという流れはとても大事なので、何度も練習をして流れを掴んでください!
まとめ
今回は、仮説検定について、実際に活用事例を紹介しながら解説していきました。
冒頭にもお話しましたが、仮説検定は一度聞いただけで完全に理解するのは難しいです。
今回は最も基本的な検定手法であるZ検定を中心に紹介しましたが、検定の種類はたくさんあるので、一つ一つ手を動かして計算しながら習得していかなければなりません。
しかし、仮説検定という概念をしっかりと理解すれば、統計学を楽しく学び続けることができると思うので、ここが踏ん張りどころだと思って、丁寧に理解することを意識しましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





