
今回は、ギャンブルと統計学のつながりについて、お話しします。
意外かもしれませんが、統計学とギャンブルは、密接した関係にあります。
なぜなら、統計学の1つである推測統計学は確率論をベースとした学問であり、その確率論はギャンブラーの疑問から始まったといわれているからです。
ギャンブルに勝つためには、感覚に頼らない正確な確率を知る必要があったからです。
そんなギャンブラーたちの疑問に答えるべく、ガリレイやフェルマーなどの偉大な数学者たちは確率論を生み出しました。
この記事を読むと分かること
- 本格的な確率論は手紙のやりとりから始まった!?
- ギャンブルの落とし穴~モンテカルロの誤謬~
- 大数の法則とは
- もっとも儲かりやすいギャンブルは
- 生粋のギャンブラー数学者:ジェロラモ・カルダノ

最後まで楽しんで読んでいただけますと幸いです!
▼▼▼ギャンブルと確率の関係をもっと知りたい方にオススメ▼▼▼
本格的な確率論は手紙のやりとりから始まった!?

(1601~1665)

(1623~1662)
本格的な確率論は、フェルマーとパスカルの手紙での意見交換から始まったといわれています。
当時ギャンブル好きだった貴族が、賭け金の配分方法についてパスカルに質問をしました。
そして、パスカルはそれをフェルマーと手紙のやりとりをしながら解決していました。
その問題が、以下のような問題です。
AとBの二人が、先に3回買った方が勝ちという勝負をした。Aが2回勝ち、Bが1回勝ったところで勝負を中止した場合、AとBの賭け金の返還はいくらにすれば公平か?(一回ごとの勝負の確率はA、Bともに1/2である。)
この問題に対する、パスカルとフェルマーの回答は、A:B=3:1で分配すればよいというものです。
何故、このような回答になるのかは、以下の図を見れば分かりやすいと思います。

3回終了時点で、Aが2勝、Bが1勝ということは、4回目でAが勝てば(1/2)ゲーム終了です。
4回目にBが勝った場合は(1/2)、互いに2勝のまま5回目の勝負の勝者が、そのままゲームの勝者となります。
つまり5回目にAが勝つ確率は、1/2×1/2=1/4
同じく、5回目にBが勝つ確率も、1/2×1/2=1/4 となります。
つまりAがゲームに勝つ確率は、1/2+1/4=3/4
Bがゲームに勝つ確率は、1/4です。
こうして、AとBの分配を3:1にすれば良いという答えを導き出しました。
本格的な確率論は、こうしたギャンブラーの小さな疑問から始まったのです。
ギャンブルの落とし穴~モンテカルロの誤謬~

1913年8月13日、モナコのモンテカルロにあるカジノで、とんでもない出来事が起こりました。
その出来事とは、なんとルーレットで26回連続偶数が出たというのです!
0~36の数字が書かれたルーレットで、偶数が出る確率は18/37です。
26回連続で偶数が出る確率は、(18/37)26で、計算すると、約1億3700万分の1という確率になります。
偶数が10回以上連続で出たあたりから、ギャンブラーたちは、狂ったように奇数に賭け始めました。
「いくらなんでもこんなに偶数が続くはずない、次こそは奇数が来る!」と考えたのです。
しかし、ギャンブラーたちの願いも虚しく、その後も偶数が出続け、最終的にカジノの運営側がボロ儲けという結果になったのです。
このように「偶数が続いたから、次は奇数が来る!」というような考え方を「モンテカルロの誤謬」もしくは「ギャンブラーの誤謬」といいます。
ルーレットでは、前の試行が何であろうと、偶数が出る確率は変わりません。
身近な例では、「子供が3人連続で男の子だったから、次は女の子だろう」といった考えもモンテカルロの誤謬の例です。
では、なぜ26回も連続で偶数が出たのでしょうか。
これには、大数の法則が関係しています。
大数の法則とは
大数の法則とは、偶然の出来事を何度も繰り返せば繰り返すほど、本来の確率に落ち着いていく、という法則です。
乱数メーカーを使って考えてみましょう。
まず、設定として、0と1という2つの数字がランダムで出るようにしています。
それぞれの数字が出る確率は1/2です。
それでは、10個の乱数を出してみましょう。
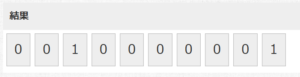
10個の乱数を出した結果、0が8個、1が2個という少し偏った結果になりました。
次に100個の乱数を出してみましょう。
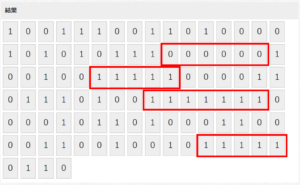
100個の乱数を出した結果、なんと0が50個、1が50個となりました。
ここまでピッタリ半々となったのは偶然ですが、試行回数を増やすほど、本来の確率に近づいていくというイメージはなんとなく掴めたのではないでしょうか。
他の例を挙げると、これがもしサイコロだった場合は、試行回数を増やせば増やすほど、それぞれの目が出る確率が1/6に近づいていくということです。
さて、100個の乱数を出した図で、1/2の確率にもかかわらず、最大で7回連続1が出たところがありますね。(5連続以上同じ結果が出た箇所を赤枠で囲っています。)
最終的には、1/2の確率に近づいていくのですが、その過程ではこのように偶然同じ結果が長く続くことも十分考えられるのです。
カジノの歴史は長く、その歴史のなかで幾度となくルーレットは行われてきたはずです。
そのため非常に珍しいことではありますが、26回連続で偶数が出ることも、起こりうることなのです。
もっとも儲かりやすいギャンブルとは
ギャンブルには、以下のように様々な種類があります。
①パチンコ・スロット
②公営競技(競馬、競艇、競輪、オートレース)
③カジノ
④宝くじ
厳密にはもう少し細分化することが可能ですが、今回はこの4種類について考えてみます。
早速ですが皆さん、上記の4つのギャンブルの中で、もっとも儲かりやすいギャンブルは一体どれだと思いますか。
この答えは、ギャンブルの期待値(還元率)から考えることが出来ます。
ギャンブルにおける期待値とは、賭けた金額が一回の試行でどれほど返ってくるかという利益率を指します。
たとえば、期待値が120%なら、100円賭けたときに120円のリターンがくることが予想される、ということを示しています。
それでは、さきほどの4つのギャンブルの期待値を見ていきましょう。
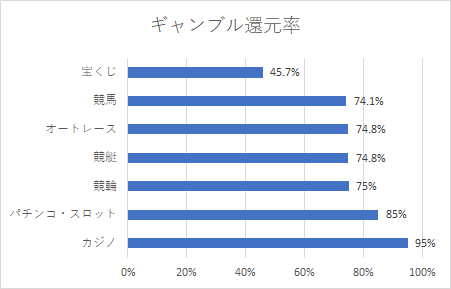
上のグラフから見て、還元率が良いのは、上から順番に「カジノ→パチンコ・スロット→公営競技→宝くじ」となります。
ギャンブルは運営元が儲からなければ成立しないので、当然ながら100%をこえる期待値のものはありません。
なかでも、宝くじの期待値は50%以下と飛び抜けて低いことが分かります。
年末に多くの方々が宝くじを買いますが、この期待値を知って買っている人がどれだけいるのでしょうか。
いずれにしろ、ギャンブルをせずに堅実にお金を貯めるのが、お金持ちへの近道なのかもしれません。
生粋のギャンブラー数学者:ジェロラモ・カルダノ

ジェロラモ・カルダノ(1501~1576)は、ミラノ出身の数学者です。
三次方程式の虚数の概念を用いるなど、代数学の業績で知られるカルダノですが、実は彼は非常に金遣いの荒いギャンブラーでもありました。
彼はギャンブルに勝つために、確率論を用いてギャンブルに挑みました。
これが現在の、確率論をベースとした推測統計学につながったとされています。
ちなみに、偉大なギャンブラー数学者カルダノは、こんな名言を残しています。
「ギャンブラーにとって最大の利益はギャンブルをしないことだ」
確率論を確立するほどギャンブル好きだった彼の言葉は、非常に説得力がありますね。
最後に
さて、今回はギャンブルと統計のつながりについてお話ししました。
ギャンブルと統計は、過去のデータを基に未来を予測する、という点でもそれぞれ共通点があります。
そのため、多くのギャンブル好きの学者が必勝法を探しましたが、当然ながらギャンブルの必勝法は現在見つかっていません。(というか必勝法があるなら、それはギャンブルではないですよね)
どれだけ推測統計が発達しても、確実な予想ができないからこそ味わえるあのワクワク感は大切にしたいものです。
▼▼▼ギャンブルと確率の関係をもっと知りたい方にオススメ▼▼▼
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





