
今回は、統計の基礎である代表値について解説していきます。
代表値は、統計検定3級でかなり問われやすいテーマですので、この機会にしっかり覚えておきましょう!
この記事を読むと分かること
- 代表値とは
- 代表値の種類
- 代表値とヒストグラムの関係
- 代表値の注意点

最後まで楽しんで読んでいただけますと幸いです!
代表値とは?
何千何万とある、膨大なデータの特徴を「一目で知りたい!」「簡潔に伝えたい!」となったとき、皆さんならどうしますか。
おそらく真っ先に思い浮かぶのが、「グラフ化」ではないでしょうか。グラフは、視覚的に特徴を捉えることが出来るので、データの分布もイメージしやすく、非常に有効な手段だと言えます。
では、ノートや黒板がなく、グラフが書けない場面だったらどうしますか。
そんなときに便利なデータの特徴を表す指標が代表値です。
代表値は、データ全体の特徴を表す(代表する)値のことです。
グラフ化よりも、さらにデータの特徴をシンプルに把握でき、簡潔に伝えることが出来る値です。
代表値の種類
代表値は、以下のように3種類に分かれます。
- 平均値
- 中央値
- 最頻値
それぞれの特徴をざっくりまとめると以下の図の通りになります。
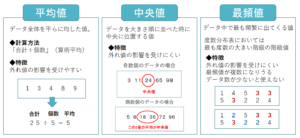
代表値は、データの特徴を表す方法として有効ですが、一つの代表値だけでは、データの特徴を表すには不十分な場合もあります。
複数の代表値を組み合わせると、より詳しくデータの特徴を把握することが出来るようになります。
それでは、それぞれの代表値について例を挙げながら説明していきます。
平均値(アベレージ)
平均値は、小学校で習うので有名ですね。
※平均には様々な種類がありますが、一般的に「平均」というと、算術平均のことを指します。
平均値は、「合計÷個数」で求めることができます。具体例で考えてみましょう。
たとえば、5人の学生がいたとします。
彼らの身長が、それぞれ「170cm、167cm、174cm、171cm、178cm」だったとします。
そうすると、彼らの身長の平均値は (170+167+174+171+178)÷5=172cm ということになります。
このように考えると、平均値は文字通り、データ全体を平らに均(なら)した値ということが分かります。
平均値のメリット・デメリット
平均値のメリットは、全てのデータを対象に算出する代表値であるという点です。
しかし、平均値にはデメリットもあります。
それは、平均値は外れ値の影響を受けやすいという点です。
(外れ値とは、極端に大きかったり小さかったりする値のことです。)
具体例で考えていきましょう。
たとえば子供が3人いるとします。
その子たちの毎月のお小遣いは、それぞれ300円、400円、500円です。
そうすると、お小遣いの平均は、(300+400+500) ÷ 3 = 400円 です。
そこへ、毎月1万円もらっているお金持ちのお坊ちゃんが加わりました。

すると、どうでしょう。
彼らのお小遣いの平均は、(300+400+500+10,000) ÷ 4 = 2,800円となります。
4人中3人が、300~500円しかもらっていないのに、一人ずば抜けて多くもらっている子が現れたことで、平均値が一気に上がってしまいました。
これでは、データの特徴を表している値だとは言えませんよね。
このようにデータの中に外れ値が含まれていると、その影響で正しいデータの特徴を表しにくくなることが、平均値のデメリットです。
中央値(メジアン)
中央値とは、データをデータを大きさ順に並べた時に中央に位置する値のことです。
具体例を挙げると、 4,1,5,3,2 という5つのデータがあったとします。
このデータを小さい順に並び替えると、1,2,3,4,5 です。
つまり、この中で真ん中に位置する値は3なので、中央値は「3」ということになります。
すごくシンプルですね。
では、このような場合はどうでしょう。
1,2,3,4,5,6 という6つのデータだった場合です。
この場合、データの真ん中といってもデータが偶数個のため、真ん中が分かりません。
このような場合は、真ん中に最も近い2つの値の平均値が、中央値となります。
つまり今回の場合、1,2,3,4,5,6の中で真ん中に最も近い数字は3と4ですよね。
つまり、この2つの平均ということは(3+4) ÷ 2 = 3.5 なので、中央値は「3.5」となります。
中央値のメリット・デメリット
中央値のメリットは、外れ値の影響を受けにくいという点です。
先ほどの子供3人のお小遣いの例を思い出してみましょう。
お小遣いが300円、400円、500円の3人の中央値は400円です。
ここに、お小遣い1万円お坊ちゃんが加わったとしたらどうでしょう。
それぞれのお小遣いは、300円、400円、500円、10,000円となるため、真ん中に近い2つの値は400円と500円。
その平均をとることになるので、中央値は450円ということになります。
先ほどの平均値では、お坊ちゃんが入ったことで400円から2,800円に跳ね上がってしまいましたが、中央値では、400円が450円になって、多少の影響は受けているものの、その影響はかなり小さいですよね。
これが外れ値の影響を受けにくいという中央値のメリットです。
しかし、このメリットは、裏返すとデメリットでもあります。
それは、データそれぞれの中身を十分に活用出来ていないからです。
たとえば、すごく難しいテストが実施されたとします。それを受けた5人の結果は、20点、23点、30点、37点、100点だったとします。100点だけ明らかに突出している外れ値です。
ほかの子たちの点数と比べると、「100点の子は頭がいい」もしくは「すごく努力して成績が伸びた」など、データから予測することができます。
外れ値は、平均を狂わせる要素でもありますが、特徴的なデータとして、それがあることを見逃してもなりません。
しかし、中央値だけでみると、真ん中の30点になるので、100点という突出した特徴を見逃してしまいます。
最頻値(モード)
最頻値とは、その名の通り最も頻繁に現れる値のことです。
たとえば、以下のような数字10個のデータがあったとします。
2,8,7,1,4,7,3,9,5,7
この場合、7だけが3回出てきており、そのほかの数字は1回ずつしか出てきていません。
そのため、最も頻繁に現れる値、最頻値は「7」ということになります。
では、これがもし以下の通りだったらどうなるでしょうか。
2,8,7,1,4,7,3,9,5,4
この場合、7と4が二回出てきており、そのほかの数字は一回ずつです。
そのため、最頻値は「4」と「7」ということになります。
最頻値のメリット・デメリット
最頻値のメリットは、中央値同様、外れ値に強いという点です。なんせ外れ値というくらいですから、めったに同じ値の外れ値は現れません。そのため、最頻値として現れて分析の邪魔をしてくる、ということがありません。
しかし、そんな最頻値にもデメリットはあります。
1つは、最頻値が複数になる場合があることです。
平均値や、中央値は1つの値しかとりません。しかし、最頻値はあくまで最も頻繁に現れた値なので、頻度が同じであれば、複数になり得るのです。
このことは、先ほど上で挙げた最頻値の例からも分かると思います。
代表値は、数多くのデータの特徴をなるべくシンプルに表すためのものでした。もし、代表値である最頻値が、3個も4個も出てきたらぶれちゃいますよね。代表がいくつもあると、代表としての意義が薄れます。そのため最頻値がたくさん出てきてしまうと、代表値としての有用性も薄れてしまうのです。
そして、もう一つのデメリットは、データ数が少ないと使えないということです。
これは、平均値、中央値でも使った「4人の子供のお小遣い」の例で考えてみましょう。
それぞれの子供の毎月のお小遣いは、300円、400円、500円、10,000円でしたね。
この場合、300円も、400円も、500円も、10,000円も全て一度ずつしか出てきていません。
つまり、全てが最頻値となってしまいます。
これでは代表値の意味がありませんよね。
データ数が少ないと、このようなことが起こりやすく、最頻値が使えなくなります。
代表値とヒストグラムの関係
それぞれの代表値には、メリット・デメリットが存在します。
特にメリット・デメリットが顕著になりやすいのは、特徴的な分布やデータが現れた場合が多いことです。
具体例として、3つのパターンの分布の場合を見てみましょう。
まず、下の図のような山が一つ(単峰性)で左右対称の分布では、平均値,中央値,最頻値はほとんど同じ値になります。
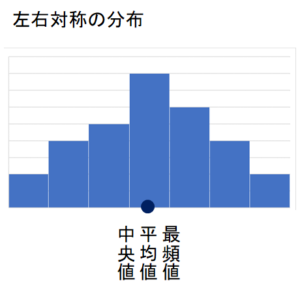
そのため、どの代表値を使っても問題ないことが多いです。
続いて、山は一つですが、左にデータが偏っており(非対称)、右に裾(すそ)の長い分布です。
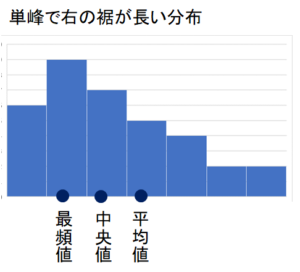
上のような図では、平均値が外れ値に引っ張られるため、「最頻値,中央値,平均値」の順に並ぶことが多いです。
分布の形によって、代表値同士の大小関係も変わってくるということですね。
そして3つ目に、山は一つですが、右にデータが偏っており(非対称)、左に裾(すそ)の長い分布です。
このような場合は、「平均値,中央値,最頻値」の順に並ぶことが多いです。
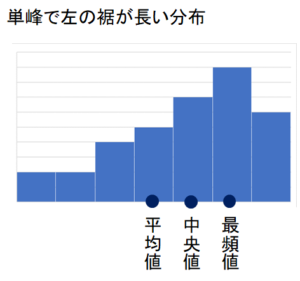
この部分は、統計検定でも問われやすい部分ですので、覚えておくと便利です。
代表値の注意点
代表値はデータの特徴を表すうえで重要な指標の1つですが、一つの代表値だけで「これがデータの特徴だ!」と断言するには少し力不足です。
これまでにお伝えした通り、各代表値にはメリット、デメリットが存在します。
そのため、例えば平均値だけをみて、データの特徴をつかんだ気になる、というのもよくありません。
活用時には、複数の代表値や図などと組み合わせながらデータの特徴を探っていくといった慎重さが大切になってきます。
若者の貯金額と代表値
よく代表値の危うさを表した事例として、若者の貯金額についてのデータが挙げられるので、ご紹介します。
金融広報中央委員会による「家計の金融行動に関する世論調査[単身世帯調査] 令和3年」という調査によると、20代単身世帯の貯金額は、平均が113万円となります。
「そんなにあるの!?」と思った方もおられるかもしれません。
ここで中央値を見てみると、中央値では8万円という結果になりました。
つまり、一部の凄く稼いでいる方々に引っ張られて平均値が引き上げられているということが分かります。
このように、片方の代表値のみを使ってしまうと、正しい姿を見れない可能性がありますので、注意が必要です。
まとめ
少し長くなってしまったので、あらためて3つの代表値をまとめましょう。
代表値の種類
- 平均値:データ全体をならした値
- 中央値:中央に位置する値
- 最頻値:最も頻繁に現れる値
ポイント
- 代表値にはそれぞれメリットデメリットがあるため、それらを考慮したうえで活用することが大切。
- 代表値とはいえど、1つでデータの特徴を正しく捉えることは危険。
- 複数の代表値を組み合わせて、正確なデータの特徴を捉えることが大切
今回出てきた3つの代表値は、どれも統計学では当たり前のように使われる言葉です。
この機会に是非覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





