データ変数の関係性を評価する数字である決定係数は、回帰モデル（線グラフ）にとってなくてはならない重要な指標です。
異なる側面を持ちながら相関係数と重なるアイデアを持っています。
そのため、決定係数と相関係数がどう違うのかを理解している方は少ないのではないでしょうか。
「決定係数ってなに？」
「決定係数を用いた例をしりたい」
「相関係数とはどう違うの？」
そんな方はいらっしゃると思います。
そこで当記事では、決定係数の概要と公式を用いた例、相関係数との関連について紹介します。
決定係数とは
決定係数（英：Coefficient of Determination）は、データに対して計算された予測値がどれだけ正しいかを評価する指標のことです。
別名、寄与率とも言われ、その数字が大きいほど予測モデルが説得力を持つようになります。
予測値を、実際の観測値をyとしてとります。
（予測値：は最小二乗法で求めることができる直線の式）
通常、決定係数はR²またはr²という記号で表されます。
決定係数がとる範囲
決定係数：R²がとる範囲は、基本的にの範囲になります。
0に近い、または0に等しいとき
・その予測モデルは実際の観測データを説明できていないことを示します。
1に近い、または1に等しいとき
・その予測モデルは観測データの関連性・予測を説明できる、精度の高いモデルであることになります。
0から1の間をとるとき
・その予測モデルは観測データの一部を説明・予測できていることを示します。
R²が0.7を超えるとその決定係数R²は説得力があると言われます。
「基本的に」をとる範囲になると説明しましたが、必ずしもその範囲をとるとは限りません。いくつかの例では、決定係数が0よりも小さくなる数値になることがあります。
決定係数の求め方
R²を求める一般的な式は、以下の通りです。
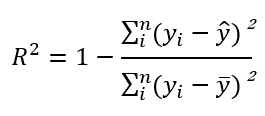
上記の式のなかにある
が示すものは、「予測直線とそれぞれの点との距離（残差）」を二乗してすべて足したものになります。
また、
が説明していることは、直線を引く前の、「ある距離からのばらつき（偏差）」を足して二乗したものです。
Σ：シグマは合計を意味します。
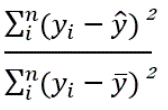の数値が小さいほど決定係数の数値が大きくなり、予測モデルが説明力をもつと定義されます。
上記の分数の式は、分母が分子よりも大きくなるため、1を超える数値になることは少ないです。
しかし、例外もあるので紹介します。
R²=0, R²<0になる場合
極端なケースになりますが、の場合にR²=0になります。
つまり、予測モデルの直線が実際の観測データの平均と一致してしまうときです。
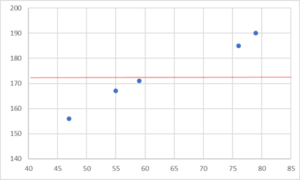
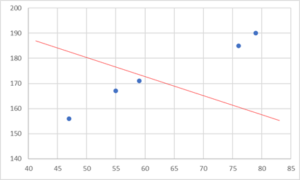
一方で、R²<0になる場合は、右上になる相関がありそうなのに右下に続く予測直線を引いてしまった場合です。
決定係数を使う例
想像しやすい例として体重と身長についてデータを決定係数を用いながらもとめてみましょう。
身長は体重に影響を及ぼすのかを検証するために、とある学校で生徒5人に対して身長・体重の測定が行われました。
体重をx、身長をyとします。
| 体重（x） | 身長（y） | |
| 59 | 171 | |
| 79 | 190 | |
| 76 | 185 | |
| 47 | 156 | |
| 55 | 167 | |
| 平均 | 63.2 | 173.8 |
グラフにして整理すると、以下のようになります。
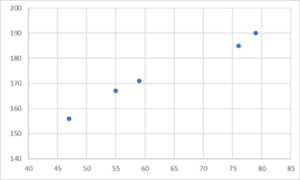
このデータ変数に対して、最小二乗法を使って予測のための直線を引いていきます。
最小二乗法を利用すると、
の直線の式を手に入れることができます。
この直線の式をグラフに当てはめると、
ここから決定係数を用いて、予測のための直線と実際の点がどれだけマッチしているのか計算していきます。
上記の公式を参考にして、
 |  | |
| 2.5281 | 7.84 | |
| 0.6241 | 262.44 | |
| 1.5376 | 125.44 | |
| 2.3409 | 316.84 | |
| 2.4025 | 46.24 | |
| 合計 | 9.4332 | 758.8 |
それぞれの合計の部分を、分子・分母に当てはめていきます。
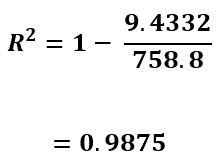
以上の式と表から決定係数0.9875という数値を手に入れることができました！
0.9875という数値は1にかなり近いため、予測のための直線は実際の数値に対して大きな説得力を持つということになります。
相関係数との関連とは
実は決定係数は相関係数：rを二乗しても手に入れることが可能です。
そのため、
という関係性が成り立ちます。
反対に、決定係数を平方すると相関係数を手に入れることができるということです。
試しに、上記の身長・体重の例に関して解いてみましょう。
相関係数の公式と共分散を用いて、相関係数の値を計算すると
が手に入ります。
その数値を二乗すると、
となり、これは以下の数値とほとんど一致します。（有効数字ごとに若干のずれが生じますが問題ありません。）
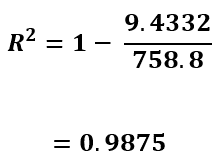
興味深い共通点ですね！
加えて、であるため、そのデータ変数は正の相関を示すということにもなります。
まとめ
当項目では、決定係数についての概要と公式、使用する例と相関係数とのつながりについて紹介しました。
決定係数は、予測モデルが実際の観測とどれだけ合致しているのかを測る指標です。数字が1に近づくほど大きな説得力を持つと定義されます。
しかし、決定係数だけで予測モデルが正しいと判断するのは避けましょう。なぜなら、データの関連性・規則性はさまざまな要因が絡み合っているからです。
相関係数とは違ったアプローチでデータに対する分析を行いますが、決定係数は相関係数を二乗した数であるという興味深い点があります。
決定係数は予測モデルがどれだけ説得力をもつか、相関係数はそれぞれの変数間の関連正と方向を評価するという違いを理解していきましょう。
こちらが参考にする文献にURLになります。
（参考）
- https://sigma-eye.com/2018/10/22/the-coefficient-of-determination/
- https://bellcurve.jp/statistics/glossary/1289.html
- https://manabitimes.jp/math/1016
- https://best-biostatistics.com/correlation_regression/r-square.html
