
統計学の教科書を読んでいると、よく出てくる言葉が「中心極限定理」です。
多くの教科書の序盤に出てくる基本定理なのですが、数式や証明を読んで、すぐに理解をするのはなかなか難しいかもしれません。
また、「統計学を勉強しよう!」と意気込んでも、この中心極限定理の理解につまずき、その先に進むのを諦めてしまう方も多い難関の1つだと思います。
また、似たような意味の「大数の法則」との違いが分からない…という方も少なくないのではないでしょうか。

また、中心極限定理と大数の法則との関連性についても説明していくので、是非最後まで読んでみてください!
この記事を読むと分かること
- 中心極限定理とは
- 大数の法則との違い
- 中心極限定理の具体例
- 中心極限定理を使うメリット
中心極限定理とは?
まず中心極限定理とは、何なのでしょうか。
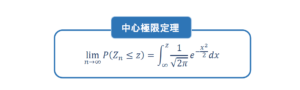
中心極限定理は、統計学の教科書などでは以下のように説明されています。
“Xが平均μ、標準偏差σのある分布に従うならば、大きさnの無作為標本に基づく標本平均の分布は、nが十分に大きい時、平均μ、分散σ²/nの正規分布に近づく”
これだけ聞くと、統計学になれていない方ですとチンプンカンプンかもしれません。
数式はもちろんのこと、説明部分にも「無作為標本」「標本平均」など聞きなれない言葉がたくさんあって、結局のところ何を表しているのか分かりづらいですよね。
上記の説明をシンプルに表現すると、「元の分布がどんな分布でも、そこからとってきた標本の分布は回数を増やすほど正規分布に近づいていく」といったイメージです。
ここからは中心極限定理が使われている身近な例を紹介しながら、中心極限定理の意味やメリットについて説明していきたいと思います!
身近に存在する中心極限定理
ここからは、身近な事例をもとに、中心極限定理について考えていきたいと思います。
コインの裏表

身近に存在する中心極限定理の具体例1つ目は、「コインを投げた時の裏表」です。
コインは「表」か「裏」の2通りしか出ません。
そして、コイン投げを1回行った時には、表が出る確率は1/2、裏が出る確率も1/2となります。

さて、ここでコインを10回投げたとすると、3回表が出る確率の計算について考えてみましょう。
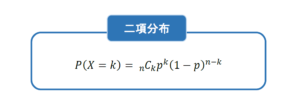
コインをn回投げた時に「表」が出た場合を成功として、表が出る確率は「二項分布」に従います。
二項分布は、試行回数n、成功する回数k、1回の試行で成功する確率pを指定することで、n回の試行でk回成功する確率を計算することができます。
しかし、二項分布を用いた確率の計算は、試行回数nを100, 1000と増やしていくと計算が少し面倒になります。
そこで出てくるのが中心極限定理です!
試しに、コインを投げる回数を1回、5回、10回、100回と増やしていった時に表が出る回数の平均値に関する分布を見てみましょう。
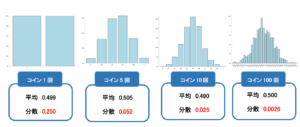
試行回数1回の場合には、全く正規分布とは言えない形をしていますが、試行回数nを増やしていくと確かに正規分布に近い形となっていますね!
二項分布の期待値と分散はそれぞれ、np、np(1-p)で表されるので、表が出る確率が1/2=0.5の場合には期待値0.5n、分散0.25nとなります。
また、コイン投げ1回を行った時の期待値と分散はそれぞれ、0.5と0.25になるので、これが母集団の期待値と分散に相当します。
上の図のそれぞれの分布の平均と分散を算出すると、試行回数を増やすほど、母集団の期待値である0.5、分散0.25/nの正規分布に近付いていることが分かります。
サイコロの目の平均
正規分布とはの記事でも紹介しましたが、サイコロの出た目の平均値も中心極限定理によって正規分布に従うことが知られています。
サイコロの場合は、1回の試行ではそれぞれの目がでる確率が1/6ずつとなっています。
サイコロのそれぞれの目が出る確率は、以下のような「一様分布」と呼ばれる分布に従っています。
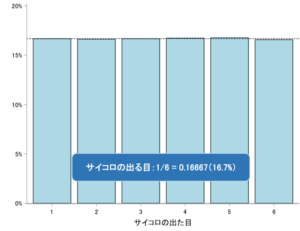
サイコロを1回振った時の出た目の分布は正規分布の形とは似ても似つきません。
しかし、サイコロを振る回数を5回、10回と増やしていった場合どうなるでしょう。
実は、振る回数を増やすほど出た目の平均値の分布は正規分布に近い形になります。
このように、元の分布がどのような分布であっても、試行回数nを増やしていくと正規分布に近づいていくのが中心極限定理の重要な性質です!
中心極限定理を使うメリット
中心極限定理についてイメージはついたけど、使うメリットは何なのか、と思う方もおられるかもしれません。
中心極限定理には、大きく分けて以下の2つのメリットが存在します。
メリット1. 計算が楽
中心極限定理は、試行回数を増やすと正規分布に近づいていくということは分かったけれども、それがどんなメリットになるの?と思う方もいらっしゃるかもしれません。
ズバリ、中心極限定理を使うメリットは、平均や分散、ある値となる確率がすぐに算出できることです!
先ほどのコインの例を用いると、1万回繰り返しコイン投げを行った時に表が出る確率を二項分布を用いて計算しようとすると、計算量がとても多くなり、時間がかかってしまいます。
そこで、中心極限定理によって正規分布に近づくことを利用すれば平均や分散がすぐに描けるので、コインを1万回投げた時に表が出る確率をすぐに出すことができるのです。
メリット2.母集団の推測が出来る
もう1つのメリットとしては、母集団の分布が分からなくても標本の分布から母集団の平均などを推測することができるという点です。
中心極限定理は、”母集団の分布がどのような分布であっても”母集団から取り出した標本の平均の分布は正規分布に近づくという性質があります。
今回紹介した例では、元の分布が二項分布や一様分布に従っていることが分かっていました。
しかし一般には母集団の分布が分からない状態で、標本の分布の平均や分散を利用しながら推測していくケースが多いです。
その際に中心極限定理を用いて正規分布であることを仮定すると、平均や分散が容易に算出できるので、区間推定や仮説検定での評価が楽にできるようになります。
区間推定や仮説検定についての詳細な説明は、また別の機会にしたいと思います。
中心極限定理と大数の法則の関係性とは
多くの人が同じものだと解釈してしまいがちなのが「中心極限定理」と「大数の法則」です。
たしかに両者の意味は似ているのですが、微妙に立ち位置が異なります。
2つの法則にどういった関係性があるのか、簡単に説明していきたいと思います。
まず、大数の法則は、統計学の教科書などでは以下のように説明されています。
“平均μ、分散σ²の分布に従う確率変数について、その標本から求められた経験的な期待値と真の期待値の誤差εは、サンプルサイズnが大きい時に0に近づく”

こちらも数式を見るとゾッとしてしまうかもしれませんが、意味していることはシンプルです。
要は、「標本の数(試行回数)が増えるほど、標本の中で算出したある事象が発生する確率が、本来事象が発生する確率に等しくなる」ということを言っています。
中心極限定理も、標本の数(試行回数)が増えるほど、母集団の期待値に近づいていくということを示しているので、大数の法則とほぼ同じことを言っていますね。
しかし、先ほどのメリットでも説明しましたが、中心極限定理は”母集団の分布がどのような分布でも、標本の分布は正規分布に近づく”という性質が追加されているので、中心極限定理は大数の法則の中に含まれる一例であるといえます。
大数の法則についてもっと知りたい方は以下の記事をご覧ください!
統計学はギャンブルから生まれた!?統計学とギャンブルの意外なつながり
まとめ
今回は中心極限定理について、身近な例を用いながらどういった定理なのかを説明しました。
中心極限定理自体は単純なものですが、数式で表すと解釈しづらくなってしまうと思います。
ですので、なるべくコインの裏表の図などの具体例で思い出してみると良いと思います。
また、中心極限定理は大数の法則の中に含まれる1例のようなものであり、中心極限定理を使うことで母集団の平均や分散が推測しやすくなることがメリットであるというお話をしました。
このメリットはこれから統計学を勉強していく上でとても大事になっていくものなので、是非覚えてもらえたらと思います!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





