
いきなりですが、「有意差がある」「有意差がない」という言葉を聞いたことはありますか?
統計学を学んでいないと、なんとなく「有意な差でしょ」くらいに思っている方が多いのではないかと思います。
また、「有意差が見られるような結果が得られれば良し!」と考えている方も多いと思うのですが、「そもそも有意差が何を表しているのか分からない…」という方も少なくないと思います。
そこで今回は「有意差」とは何か、有意差があるかどうかを見極めるために必要な過程やその解釈について、分かりやすく解説していきたいと思います!
是非最後まで読んでみてください!
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- 有意差とは
- 帰無仮説、対立仮説との関連性について
- 有意差の使用例

是非最後まで楽しんで読んでいただけますと幸いです!
有意差とは
有意差とは、帰無仮説が正しいと仮定した下で、観測された値との差が誤差では済まされないような大きな差であり、統計的に意味があると言えるような差のことです。
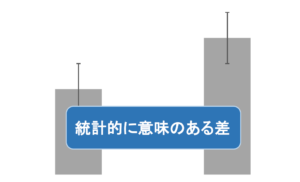
Weblio辞書では有意差をこのように定義しています。
“統計上、ある事柄の起こる確率が有意水準未満であること、つまり偶然であるとは考えにくいことをいう”
(引用)https://www.weblio.jp/content/%E6%9C%89%E6%84%8F%E5%B7%AE
「帰無仮説」「有意水準」と、難しそうな言葉が並びますが、後ほど補足説明をするのでご安心ください。
まずは身近な例を用いて有意差の概念をご紹介したいと思います。
有意差の身近な例~テストの点数~
A組、B組の2つのクラスで同じ数学のテストを実施したとしましょう。
A組の数学の平均点は80点でしたが、B組の平均点は65点でした。
この場合、2つのクラスの平均点の差は、誤差とは言い切れないほど差でありそうだと思います。
しかし、「あるクラスの数学の平均点は80点でしたが、もう一方のクラスの平均点は73点でした。」と言われたら、2つのクラスの平均点は誤差の範囲なのか、誤差では表せない大きな差なのか結論付けるのが難しいですよね。
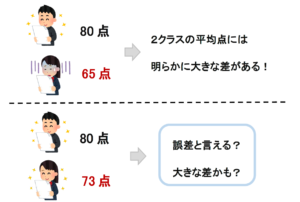
このような場合に、統計的に意味のある差だと判定されれば「有意差あり」、意味のある差だと言えなければ「有意差なし」と結論付けられます。
その他の例だと、以下のようにビジネスの場で有意差の検討が行われることも多いです。
ビジネスにおける有意差の例
- 「ある商品の不良品の発生率が高めだが、誤差の範囲といえるのか?」
- 「下半期の売上が向上したが、マーケティング戦略によるものといえるのか?」
- 「アンケート調査の年代毎の回答結果の差は有意なものといえるのか?」
有意差を求めるために必要なこと
有意差についてしっかりと理解するためには、統計的に意味のある差だと判定するために、何をしなければならないのかを知ることが重要です。
検定によって有意差があるかを判断する
有意差があるかどうかは、「検定」と呼ばれる統計処理によって判定されます。
検定についての詳細は別の記事にてお話ししますが、検定の大まかな流れはこのようになっています。
検定の流れ
- 主張したい仮説(対立仮説)とは逆の仮説(帰無仮説)の下で、その事象が起こる確率(p値)を求める
- 事前に定めた有意水準(よく用いられるのは5%)を下回っていれば、帰無仮説の下では稀にしか起こらない事象であると判断され、棄却される
- 帰無仮説が棄却されれば、対立仮説が採択されるので「有意差あり」と判断される
専門用語も多くなかなかピンとこない部分もあるかもしれませんが、ここでは有意差があるかどうかを判断する流れがこのようになっているということを理解して貰えればと思います。
帰無仮説と対立仮説
大まかな流れの説明の中に、「帰無仮説、対立仮説」という言葉がありました。
検定の説明の中で、「主張したい仮説(対立仮説)とは逆の仮説(帰無仮説)」と説明しましたが、「主張したい仮説と逆ってどういうこと?」と思う方もいるかと思います。
そこで、先ほどのテストの点数の例を用いて、帰無仮説、対立仮説を考えてみましょう。
2つのクラスの数学の平均点に有意差があるかどうかを判定したい場合には、帰無仮説と対立仮説はこのように設定されます。
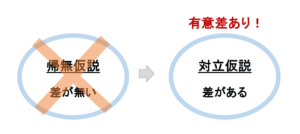
- 帰無仮説(主張と逆の仮説):2つのクラスの数学の平均点には差が”ない”
- 対立仮説(主張したい仮説):2つのクラスの数学の平均点には差が”ある”
「差が無い」という仮説を否定することができれば、それはつまり「差がある」という仮説の方が正しいということになります。
なので、有意差が見られるかどうかは、帰無仮説を棄却できるかどうかにかかっています!
先ほどの例では、2つのクラスの平均点には差が無いという仮定の下で、平均点の差が15点になる確率(p値)が極端に小さいということが確認されれば、「15点の差は稀にしか起こらないので、誤差とは言えない!」となり、帰無仮説が棄却されます。
一方で、平均点の差が7点となる確率は一定の水準よりも高いということが確認されれば、稀な事象とは言えません。
このような場合は、平均点に差が無いという帰無仮説を否定することができないので、「有意差あり」とは言えなくなります。
有意差の解釈はどうなるの?
ここまで有意差の概念や、有意差があるかどうかを見極める流れについて解説してきました。
では実際に有意差が見られた場合、または有意差が見られなかった場合にはどのような解釈をすれば良いのでしょうか?
ここからは、解釈のミスが起こりやすい場面を2つ紹介します。
有意差について適切に理解をすれば、結果のまとめ考察がしやすくなります。
以下の例を見ながら有意差の解釈について学んでもらえればと思います。
「有意差がない」=「差は全くない」という訳ではない!

検定をした結果、有意差が見られた場合には、もちろん「2つの結果には統計的に意味のある差が見られる」と言っていいでしょう。
しかし、有意差が見られなかった場合には「2つの結果には差がない」と言ってしまうと少し誤解が生じます。
有意差はあくまでも、統計的に意味のある差かどうかを評価したものです。
そのため、たとえ有意差が見られなかったとしても2つの結果に全く差が無いのではなく、「統計的に意味のある差が見られなかった」という解釈になります。
「有意差がある」=「大きな差がある」とは必ずしもいえない!
もう1つ解釈を間違いやすい例として、p値との関連があります。
「p値は0.01以下であり有意差が見られたため、2つの結果には大きな差が見られる」という記述は一見良さそうなまとめに見えますが、若干解釈のミスがあります。
P値は、帰無仮説を棄却するかどうかの判断材料なので、事前に決めた有意水準を超えているか、超えていないかを見るために使います。
有意差があることが確認されて、帰無仮説の下でその事象が起こる確率であるp値も極端に小さかったからといって、2つの結果に大きな差があるということは言い切れません。
「有意差は、統計学的に意味のある差かどうかを判断するもの」、という理解を忘れないことが、解釈を間違えないようにするポイントかもしれません。
まとめ

今回は「有意差」に着目して、有意差とはどういった概念なのか、有意差を求めるためには何をしなければならないのかについて解説しました。
だんだんと統計の専門用語が増えてきて、頭がこんがらがってしまうこともあるかと思います。
まずは、「帰無仮説」「対立仮説」の違いをしっかりと説明できるようになっておくと、仮説検定の勉強も捗ると思います!
また、有意差の解釈についても解説をしました。
もし有意差が出なくても、「有意差がなかったから良い結果ではない…」と落ち込むのではなく、「差があると思って検証したけれど、実際は統計的に意味のある差では無いと分かったことは重要な結果だ」という思考を持つことも大切です!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







