
こんにちは!統計ブロガーのにっしーです!
統計学を勉強したり統計関連の論文を読んでいると、よく目にするのが「p値」です。
何を表しているのかは分からないけど、とにかくp値が小さければ良い結果と言って良いのだろう、と思っている方も多いのではないでしょうか。
ざっくりとした解釈としては間違っていないのかもしれませんが、p値の意味や求め方をしっかりと理解していると、示された結果が何を意味しているのか深く理解をすることができます。
そこで今回は「p値」に焦点を当てて、p値の求め方や正しい使い方について解説していきたいと思います!
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- p値とはなにか
- p値の具体的な使い方イメージ

是非最後まで楽しんで読んでいただけますと幸いです!
有意差を見極めるうえで大事な「p値」
p値は、「帰無仮説の下でその事象が起こる確率」を表しています。
p値のpは”probability(確率)”を意味しているので、とても単純な意味に捉えられますが、p値の大きさによって有意差の有無を見極めることになるので、実はとても重要な値なんです!
ここで、有意差を見極めるまでの流れをおさらいしますね。
主張したい仮説とは逆の帰無仮説の下でその事象が起こる確率を計算し、稀にしか起こらないことが確認されれば帰無仮説を棄却し、有意差ありと判定します。
※有意差についてもっと詳しく知りたい方、復習したいという方は以下の記事も読んでみてください!
有意差とは 帰無仮説・対立仮説との関係性とともに分かりやすく解説
ではこの「稀にしか起こらない」というのを確認する基準はなんでしょうか?
それが事前に設定する「有意水準」と呼ばれる基準です。
有意水準は5%に設定されることが多いですが、厳しい基準の場合には1%に設定されることもあります。
この有意水準を基準として、有意水準>p値の場合には帰無仮説を棄却し、有意差ありと結論づけます。
一方で、有意水準<p値の場合には稀にしか起こらないとは言い切れないので、帰無仮説を棄却しません。

ここではP値と有意水準の関係、有意差とのつながりについて概念を理解してもらえればと思います。
p値の求め方
ここまで、P値の意味について大まかな説明をしてきましたが、実際に統計解析を行う場面ではどのような計算をしてp値を算出しているのかは分からない人も多いのではないでしょうか?
ある表を用いると、簡単にp値が求められる場合もあるのですが、今回はサイコロの簡単な例を使ってp値を実際に計算してみたいと思います!
2回連続で1の目が出るサイコロのp値

サイコロを2回振った時に、2回連続で1の目が出たとします。
何も細工がされていないサイコロであれば、何回振っても1/6の確率でいずれかの目が出るはずです。
何も細工がされていない正しいサイコロで2回連続で1の目が出る確率は、1/6×1/6 = 1/36 = 0.027(2.7%)となります。
※これがもし、2回連続で同じ目が出る確率の場合、1/36 × 6= 1/6となります。
これがp値です!
これだけ?と思う方もいるかもしれませんが、単純な場面ではこれだけで求めることができてしまうのです。
少し発展させて、サイコロを5回振った時に3回以上同じ目が出る確率を求めたい場合には、3回連続、4回連続、5回連続で同じ目が出る確率を足し合わせていけばp値を求めることができます。
p値の捉え方は有意水準によって変わる
p値自体は意外と簡単に求めることができる、ということが分かってもらえたかと思います。
少し話が逸れてしまいますが、p値を求めた後の話もしたいと思います。
先ほどのサイコロの例について、Aさんは2回連続1の目が出るサイコロはおかしいと考えています。
正しいサイコロであることを帰無仮説として、有意水準を5%と設定すると、正しいサイコロで2回連続1の目が出る確率2.7%は、有意水準5%よりも小さい値となるので、帰無仮説が棄却され、「このサイコロはおかしい」という結論になります。
一方で、有意水準を1%という厳しい基準に設定すると、実際に計算されたp値である2.7%のほうが大きい値となるので、帰無仮説が棄却されず、「サイコロはおかしいとは言えない」という結論になります。

このように、p値自体は同じでも、有意水準の設定によって結果が大きく変わってしまうこともあるので、有意水準は解析を行う前にあらかじめ決めておく必要があります!
標準正規分布表を利用して求めることもできる
サイコロの簡単な例では極端な場面の確率を求めたり、その確率を足し合わせることでp値が求められました。
一方、身長の分布のように正規分布を仮定できる場合には、標準正規分布表を用いることで簡単に求めることができます。
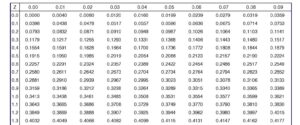
(引用)https://www.nli-research.co.jp/report/detail/id=66660?site=nli
この表の使い方や正規分布を仮定した検定の手順については、また別の機会に詳しく紹介するので、「標準正規分布表」というものを用いてもp値を求めることができるということを覚えておいてください!
p値の正しい使い方とは?
先ほど、有意水準によってp値の捉え方が変わるというお話をしましたが、実際に解析をし始めると、気づかないうちにp値の解釈や使い方を間違えてしまうこともあります。
ここからはp値の解釈や使い方について、間違えやすいポイントを2つ紹介していきたいと思います。
p値は小さければ小さいほど良い?
「p<0.01で有意差が見られ、2つの結果には大きな差があることが分かった」
このような結果のまとめ方は一見良さそうに見えますが、p値の解釈が少し間違っています。
p値は帰無仮説の下でその事象が起こる確率なので、小さければ小さいほど稀にしか起こらないという解釈ができます。
しかし、稀にしか起こらないからと言って2つの結果に大きな差があるとは言えません。
P値の大きさと実際の結果の大きさの差は同じではないことに気をつけましょう!
p値はたくさん出してはいけない?
2つの結果に差があるという仮説を立てて解析を行った結果、P値が有意水準よりも大きいために有意差なしと判定されることもよくあります。
「差があるとは言えない」という結果になると、がっかりして「きっとどこかには差があるはず!」と何回も解析を繰り返してしまう人がいるかもしれません。
しかし、そのような解析を実施すると、正しい結果を導くことができなくなる可能性があります。
統計解析(検定)を繰り返し行うということは、いくつもp値を求めて、毎回有意水準を超えるか超えないかを判断するということですが、いくつもp値を算出していると、偶然低い確率が算出されてしまうことがあります。
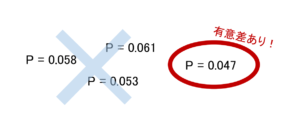
本当は2つの結果に統計的に有意な差があるとは言えない状況だったとしても、何回も解析をしてp値が一番低かった結果を採用してしまえば、「有意差が見られた」と結論付けることが出来てしまうのです!
このようなことを防ぐために、新薬開発の現場などでは、解析を行う前にあらかじめ解析方法を決めておき、結果を見てから解析方法を変えることが無いようにしています。
P値についての理解が深まると、結果を見てから自由にp値を操作するなど悪用することもできてしまうので、実際に解析を行う際には、有意水準や解析方法を事前に決めておくことが重要です。
まとめ
今回は統計解析を行う場面で頻繁に見かける「p値」について、値の意味や求め方、正しい使い方について解説しました。
P値は「小さければ良い値」というだけではなく、統計学的な有意差を見極めるために大事な値だということが分かると、解析結果の解釈も捗るかと思います。
また、p値の意味を理解していても、知らず知らずのうちに間違った使い方をしてしまうこともあるので、注意しましょう。
正しい使い方を意識しながら解析をしていくと、信頼できる解析結果を出すことができるようになることでしょう。
▼▼▼p値を徹底的に理解したい方にオススメ!▼▼▼
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





