グラフの傾向を推測する技術である最小二乗法は、季節のトレンドや科学的な実験において、データとモデルを最適化するために頻繁に用いられています。
回帰分析とも密接に関連している最小二乗法ですが、概要や使い方を理解している方はすくないのではないでしょうか。
「最小二乗法ってどう使うの?」
「公式を理解したい!」
「回帰分析とのつながりを知りたい」
そんな方もいらっしゃると思います。
そこで本記事では、最小二乗法の概要や使い方、回帰分析とのつながりについて解説します。
最小二乗法とは
最小二乗法(英:Least Square Method)は、データ値の散らばりの中で、それぞれとの誤差が最も少ない直線を見つけることを目的とした技術です。
「もっともそれらしい直線」を求めるとも言われますが、この意味は直線と点との距離が最小であり、最も適した直線のことです。
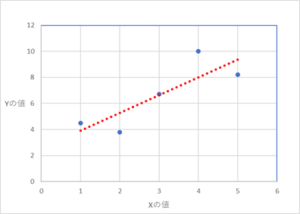
点と直線の距離が最小であるほど、データに対しての予測度が最適化されます。
統計学の中で、「推測」を行う最小二乗法は統計学らしい考えの1つと言えるでしょう。
共分散に通じる性質
最小二乗法は、共分散 に通じる面白い性質を持っています。
公式を使って説明すると複雑になってしまうため、簡略化した説明だけにします。
それは、共分散の値が正をとるとき、最小二乗法で求められる直線の傾きも正の傾きになるということです。(正の傾きとは、右斜めに進む直線のことです)
つまり共分散の値の正・負と、最小二乗法の直線の向きは対応しているということです。
実際にグラフを用いて見てみましょう。
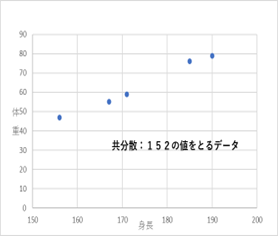
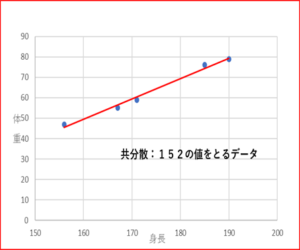
右図が最小二乗法で求めた直線です。
興味深いことに、共分散も最小二乗法も関連していることがわかりますね。
最小二乗法の求め方
最小二乗法は直線を求めるテクニックであるため、以下の式の形をとります。
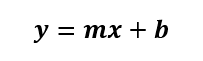
このタイプの式は多くの方が慣れている形でしょう。
次にやることは、傾き:mと切片:bの値をそれぞれ計算することです。
まず始めに傾き:mの式、
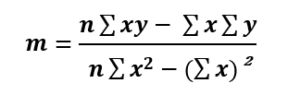
傾き:mの式でmが求まったら、その値を用いて切片:bを求めます。

傾き:mと切片:bが手に入ったら、
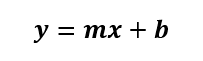
それぞれ式に当てはめて、直線の式を求めます。
Σなどの記号が多くあり一見複雑そうな式ですが、実は非常に単純な公式の1つです。
表とグラフを使って計算するとグッと分かりやすくなるので、下記の「最小二乗法の使い方」を参考にしてみてください。
最小二乗法の使い方
例として、植物の成長速度と日数をもとにした、植物の成長予測の直線を最小二乗法をつかって求めてみましょう。
Xを日数、Yを植物が成長した値とします。
表にして整理すると、
| X | Y | |
| 1 | 4.5 | |
| 2 | 3.8 | |
| 3 | 6.7 | |
| 4 | 10 | |
| 5 | 8.2 | |
| 合計(Σ) | 15 | 33.2 |
この二つの変数から、傾き:mを求めるために以下の式を展開します。
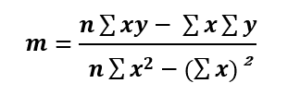
Σ(シグマ)は変数の合計を意味するので、
この式に、データセット数:n、日数:Xの合計、成長値:Yの合計をそれぞれ当てはめます。

傾き:mの値が手に入ったので、次は切片:bの値を求めていきます。


傾き:mと切片:bがそれぞれ求まったので、直線の式に当てはめていきます。
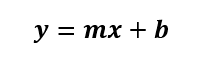
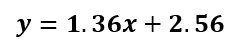
直線の式が手に入りましたね!
この式をもとに直線のグラフを作ってみると、

点と線との距離が最小で、「もっともそれらしい直線」を求めることができました。
この直線から、6日目以上の植物の成長値であっても予測が可能になります。
将来の傾向を既存のデータだけで予測を可能にする最小二乗法は、いかに強力で便利な技術であることがわかりますね。
回帰分析とのつながり
回帰分析と最小二乗法は密接に関連していますが、ほとんど同じものであると考えても間違いではないでしょう。
回帰分析は統計学の分野の1つであり、それぞれ異なった変数の関係性を数式や概念であらわす手法です。
異なった2つの変数から、さまざまな手法を用いて予測と因果関係を発見します。
一方で、最小二乗法は回帰分析で使われる手法の1つです。回帰分析は、さまざまな公式を利用してデータの予測・因果関係の発見を行いますが、最小二乗法はその中で使われる公式の1つであるということです。
最小二乗法で用いる公式と考え方は回帰分析の考え方と繋がっており、統計学的な考え方を養うことができます。
まとめ
当記事では、最小二乗法の概念と求め方、回帰分析につながりについて紹介しました。
最小二乗法は2つの連続するデータ値から、将来の傾向について予測し、それを直線で表すことができる回帰分析のやり方の1つです。
「予測」を扱う回帰分析の中の最小二乗法は、統計学的な考えを養なうことできる非常に大切なツールでもあります。
公式もかなり容易であり、初心者の方にとっても取り組みやすい公式の1つです。
実際に解きながら、最小二乗法に慣れていくことで、統計学の面白さに触れていってください。





