普段のお仕事や研究などでデータ分析をしている中で、「分散分析」という言葉を耳にしたことがある方も多いかもしれません。
しかし、いざ活用しようとしても、難しそうな数式が多く、とっつきづらいイメージを持つ方も多いかもしれません。
そこで、本記事では分散分析の特徴や使える場面、分析方法について分かりやすく解説します。
分散分析の理解を深め、実際に活用するきっかけとなれば幸いです。
分散分析とは
分散分析を使う場面
分散分析は、「見たいものに対し、効果のある要因を探したい」という場面で有効です。以下に具体例を4個示します。
- 例1 クラスによってテストの平均点に差があるかを確認したい
- 例2 高血圧の患者に降圧薬を投与し、時間が経過するにつれて血圧が下がっているといえるか確かめたい[1]
- 例3 ラーメンの「スープの味(塩、しょうゆ、味噌)」・「油の量(あっさり・こってり)」を変え、
どの組み合わせが一番美味しいのかを知りたい[2] - 例4 ある作物に対し、肥料・土を変えると収穫量に変化があるのかを知りたい[3]
このように、点数や血圧、収穫量などの「見たいもの」に対し、「これは効果があるのではないか」と仮説を立てた要因が本当に有効なのかを確認する際に分散分析を使用します。
例を見ていただくとわかるように、日常生活からお仕事、研究にいたるまで幅広い場面で活用できます。
分野に関しても、理系(工学・医学など)、文系(心理学・経済学など)問わず有効です。
データをとって何らかの行動をする必要がある時に分散分析は心強いツールとなります。
ちなみに分散分析は英語で「Analysis of variance」といい、略して「ANOVA」と表記されることもあります。
英語で表記されても慌てないよう、頭の片隅に入れておきましょう。
用語の説明
以降の説明が分かりやすくなるよう、用語を整理しておきます。
特性値
上記の説明でいう「見たいもの」のことです。
例1ではテストの点数、例2では血圧の値を指します。
因子
特性値に対し、影響があるかどうかを確認したい要因のことです。
水準
一つの因子に含まれる項目のことです。例3では、「スープの味」が因子、「塩、しょうゆ、味噌」が水準となります。
分散分析の種類
一元配置分散分析
一元配置分散分析とは、特性値に対し、因子が1種類であるケースです。
例1、2が一元配置分散分析に該当します。
二元配置分散分析
二元配置分散分析とは、因子が2種類ある場合です。例3、4のような時です。
二元配置分散分析では、それぞれの因子単独の効果に加え、2つの因子が互いに影響を及ぼし合うことにより生じる効果も見ることができます。これを「交互作用」といいます。
ラーメンの味について調査する例3を用いて交互作用を説明します。
ラーメンの味を数値化して特性値とします。
各因子、水準組み合わせにおける特性値は以下のようになったとします([2]のデータを改変)。
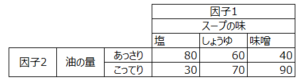
これをグラフ化すると以下のようになります。
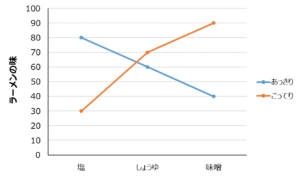
青色の折れ線グラフを見ると、油の量が「あっさり」の時は、「塩→醤油→味噌」とスープの味が変わるにつれて点数が減少していることがわかります。
しかし、オレンジ色の折れ線グラフである「こってり」の場合、真逆の傾向となっていることが分かります。
このように、片方の因子の水準のとりかたにより、もう一方の因子の効き方が異なってくるとき、「因子間の交互作用がある」といいます。
分散分析の分析方法
分散分析でできること
分散分析では、因子の水準を変化させたとき、水準間で特性値の平均に差があるといえるかを統計的に判断することができます。
クラス間でテストの平均点に差があるかを確認する例1を用いて具体的に説明していきます。各クラスに生徒が5人ずついるとします。
各クラスの生徒の点数およびその平均は以下のようになりました。
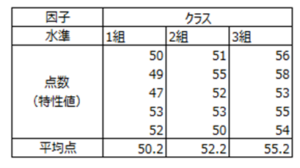
これをグラフにすると以下のようになります。
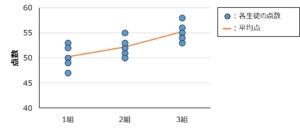
クラスによってテストの平均点に差があるといえるのでしょうか?
この結果に対し、次の2通りの考え方があります。
考え方1
確かにクラスによって点数は異なっているようにみえる。しかし、同じクラス内でも生徒による点数ばらつきがある。
このばらつきと比較するとクラス間の平均値の差は小さいと感じたから、「クラスによりテストの平均値に差があるとは言えない」のではないか。
考え方2
同クラス内の点数ばらつきと比較しても、クラス間の平均値の差は大きそうに思えます。
だから、「クラスによりテストの平均値に差があるといえる」のではないでしょうか。
分散分析をすると、上記2つの考え方どちらが正しいのかを統計的に判断することができます。
ちなみに、今回のケースで分散分析を行うと、考え方2が正しいことがわかります。
これを「統計的に有意差がある」といいます。
一元配置分散分析の計算方法
引き続き例1を用い、どのような考え方で有意差の有無を判断しているのか説明します。
詳細な計算は省き、概要を説明します。
分散分析では、「同じ水準内での特性値のばらつき」と「水準を変えたときの特性の平均値変化」を比較します。
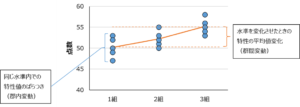
「同じ水準内での特性値のばらつき」を郡内変動、「水準を変えたときの特性の平均値変化」を群間変動とも呼びます。
郡内変動、群間変動はばらつきを表す基本的な統計量である「分散」としてその大きさを表現することができます。
郡内変動由来の分散Ve、群間変動由来の分散をVAとし、以下のようにその比をとります。

群間変動と郡内変動の比であるFAに対し、F検定という手法を用います。
これにより、群間変動は郡内変動と比較して有意に大きいかを統計的に検定することができます。
この検定で「有意に大きい」と判定された場合は、因子は特性値に対し有意に効いていると判断することができます。
「分散」を利用し、水準を変えたときの特性の平均値変化が統計的に有意か「分析」するのが分散分析なのです。
まとめ
分散分析を使える場面や分散分析でできること、計算の原理を簡単に説明してきました。
分散分析は文系・理系問わず極めて幅広い分野で効果を発揮します。非常に実用的な手法であるため、マスターすれば実際の業務や研究をスムーズに進めることができるようになるでしょう。
また、分散分析は実験計画法と呼ばれる統計的手法の根幹をなす考え方です。
本記事をきっかけとし、分散分析や実験計画法の理解を深めていただければ幸いです。
(引用)
[1] 一元配置分散分析(対応あり)─エクセル統計による解析事例 | ブログ
[2] 練習問題(30. 二元配置分散分析) | 統計学の時間
[3] 二元配置分散分析って何?【交互作用が分かります】





