
皆さんは宝くじを買ったことがありますか。
日本中が熱狂するギャンブルの一つ、それが「宝くじ」です。
サマージャンボや年末ジャンボ、などは毎年大盛り上がりで、勝っている方も多いのではないでしょうか。
さて、そんな宝くじですが買い方が複数あります。
一つは連番購入、もう一つはバラバラでの購入です。
これらの買い方違いによって、有利不利などはあるのでしょうか。
今回は宝くじの買い方について、どちらの方が有利なのかを確率を使って考えてみたいと思います。
この記事を読むと分かること
このような宝くじで、連番とバラバラでの期待値の違いを考えれば、どちらが有利かが分かります。
まずは、連番で3枚買った場合を考えてみましょう。
連番購入の場合
1~10の数字で、連番で3枚買ったときに考えられる買い方は、以下の10通りです。
「1,2,3」「2,3,4」「3,4,5」「4,5,6」「5,6,7」
「6,7,8」「7,8,9」「8,9,10」「9、10,1」「10,1,2」
それぞれの確率は等しく1/10だとします。
それぞれの買い方の当選額は以下の通りです。
- 「1,2,3」 → 0円
- 「2,3,4」 → 0円
- 「3,4,5」 → 0円
- 「4,5,6」 → 0円
- 「5,6,7」 → 100万円
- 「6,7,8」 → 100万円
- 「7,8,9」 → 100万円
- 「8,9,10」 → 0円
- 「9,10,1」 → 0円
- 「10,1,2」 → 0円
つまり10通りあるうちの3通りで100万円が獲得できるということですので、
期待値は以下のように求められます。
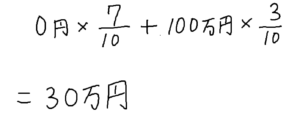
つまり、このような宝くじの場合、連番で購入した場合の期待値は30万円です。
バラバラで購入した場合
次に、ばらばらで購入した場合を考えてみましょう。
ばらばらで3枚購入する場合は、![]() =120通りです。
=120通りです。
7が含まれない、ハズレの場合の数は![]() =84通り
=84通り
つまり、7が含まれる(当たり)場合の数は、「120 - 84 = 36 通り」となります。
ここから期待値を求めると、以下のようになります。
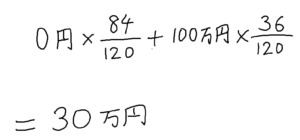
ばらばらで購入した場合の期待値も30万円になりました。
これは今回のようなケースだけに当てはまるわけではありません。
気になる方は、当選番号や当選金額、購入枚数など条件を変えて計算してみてください。
世間一般の宝くじの方式では、連番やバラバラなどの買い方によって、期待値には差が出ないようになっています。
つまり、どう買おうが宝くじに有利不利はないのです。
宝くじの還元率
ちなみに、宝くじの還元率(100円買ったときに返ってくることが期待される金額)って何%かご存じですか。
実は宝くじの還元率は50%を下回っています。
宝くじに限らず、基本的にギャンブルは大元が儲からなければ成り立たない娯楽なので、期待値はどれも100%を超えることはありません。
しかし、そのほかのギャンブルと比較しても、宝くじの還元率は圧倒的に低いのです。
一番私たちになじみ深いギャンブルである宝くじの還元率がここまで低いというのは驚きです。
ちなみに、そのほかのギャンブルについて、統計学とのつながりとともに以下の記事で解説しています。
気になった方は是非読んでみてください!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







