
こんにちは!統計ブロガーのにっしーです!
今回は「カイ二乗検定」について解説していきます!
これまでZ検定やt検定について解説していきましたが、カイ二乗検定はこれらの検定とは少し違う特徴を持つ検定手法です。
しかし、Z検定やt検定と同様、データ分析をするうえで頻繁に利用される検定手法の一つでもあります。
詳しい使い方やZ検定やt検定との違いをしっかり理解できるように、是非最後まで読んでみてください!
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- カイ二乗検定ってなに?
- カイ二乗検定の具体的な手順
- 自由度ってなに?
カイ二乗検定とは
まずは、カイ二乗検定とはどういう検定手法なのかを詳しく説明していきます。
カテゴリカルデータの検定
カイ二乗検定は、カテゴリカルデータに関する検定手法の1つです。
カテゴリカルデータとは、例えば「朝食を食べたか、食べていないか」という2つの選択肢で表されるものや、5段階のアンケート調査の結果など、値が連続していない変数のことを言います。
これまで紹介してきたZ検定やt検定は、身長や工場の部品の重さなど、0.1cm、あるいは0.1mmなどの細かい範囲で値が連続しているような変数に対して用いる検定手法でした。
一方で、カイ二乗検定は、値が連続していない変数同士に関連があるかどうかを調べるために用いる検定手法となっています。
この後、具体例を用いてカイ二乗検定の流れを解説していきます。
まずはカイ二乗検定が「カテゴリカルデータ同士の関連を調べるため」の検定手法だということを押さえておいてください!
自由度の考え方
ここで少し細かい話に入りますが、t検定など他の検定手法でも度々出てくる「自由度」についてお話したいと思います。
何を表しているかは分からないけれど、とりあえず定義に従って計算したものを使っているという人も多いのではないでしょうか。
自由度の意味が曖昧なまま勉強を進めていても理解が不十分になってしまうと思いますので、ここで一度自由度について解説します。
自由度は、一言で表すと「自由に決めることができるデータの数」です。
例えば女性10名、男性10名に対して、甘いものが好きか嫌いかアンケートを取った時に、甘いものが好きな人も嫌いな人も10人ずつ均等に分かれたとします。
この場合、女性10名、男性10名、甘いものが好きな人10名、甘いものが嫌いな人10名という情報を表にまとめるとこのようになると思います。
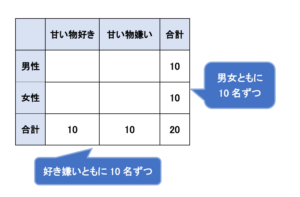
この段階では、空欄部分の「甘いものが好きな女性」の人数や「甘いものが苦手な男性」の人数は自由に決めることができる状況ですが、試しに「甘いものが好きな女性」の人数を6人と設定してみます。
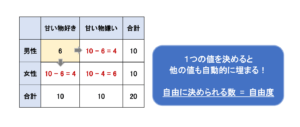
すると、自動的に「甘いものが嫌いな女性」は4名、「甘いものが嫌いな男性」は6名、「甘いものが好きな男性」は4名ということが分かってしまいます。
つまり、この場面では完全に自由に設定することができる値は1つのみとなります。
これが自由度です。
この後にも出てきますが、カイ二乗検定の自由度は(m-1)×(n-1)で表されます。
mとnは先ほど示した表の行と列に対応しています。
行も列も2つの場合には(2-1)×(2-1)=1×1=1となり、自由度は1と求められます。
カイ二乗検定の手順を具体例で解説
先ほど出てきた「甘いものが好きか嫌いか」というアンケート調査の例を使って、甘いものの好き嫌いと性別には関連があるのかどうかカイ二乗検定を用いて仮説検定を行っていく手順を紹介していきたいと思います!
この方法は「独立性の検定」とも呼ばれ、帰無仮説が「甘いものの好き嫌いと性別には関連がない(=独立している)」となります。
今回は有意水準5%として、カイ二乗検定を行っていきます。
分割表の作成
まずは、アンケート調査でどのような結果が得られたのかをまとめていきましょう。
自由度の解説でも表がいくつか出てきましたが、カテゴリカルデータを集計する時には「分割表」や「クロス集計表」と呼ばれる表を作成します。
分割表は行と列からなる表で、それぞれのカテゴリーごとの人数が一目で分かるようにまとめられた表となっています。
今回の例では、このような結果が得られたとします。
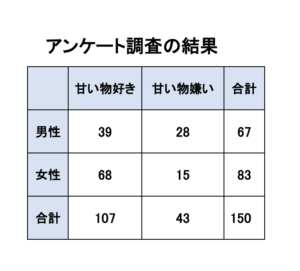
自由度の説明で用いた人数とは違いますが、この結果から、甘いものの好き嫌いと性別には関連がないと言えるのかどうか仮説検定を行っていきます。
期待度数を計算
仮説検定では、帰無仮説の下でその事象が発生する確率を計算することで、有意差があるかどうかを判断していました。
カイ二乗検定も同じ手順で進めていくため、甘いものの好き嫌いと性別には関連がないという帰無仮説の下では、それぞれのカテゴリーに何人ずつ入りそうかを予測する必要があります。
この値は「期待度数」と呼ばれ、カイ二乗検定では、期待度数と実際に観測された値の離れ具合によって、帰無仮説を棄却するような大きな差かどうかを判断していきます。
例えば、Aと書かれたセルの期待度数はこのような計算式で求めることができます。
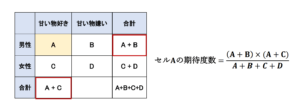
同じようにして、それぞれのカテゴリーの期待度数を計算した結果と実際に観測された値を並べてみるとこのようになります。
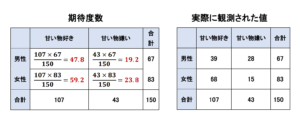
カイ二乗値を求める
ここからが検定の本題になります!
計算で求めた期待度数と実際に観測された値の離れ具合によって、帰無仮説を棄却するような大きな差かどうかを判断していきますが、この離れ具合にあたるのが「カイ二乗値」です。
正確には、(観測された値-期待度数)を2乗して期待度数で割った値を全てのカテゴリーで足し合わせることで求められます。
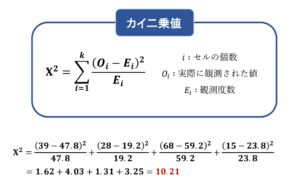
今回の例では、1.62+4.03+1.31+3.25となり、カイ二乗値は10.21となります。
あとは、カイ二乗分布表やExcelなどのツールを活用して、有意水準との比較をし、有意差が見られるかどうかを判断するだけです!
カイ二乗値からp値を求める際には、先ほど解説した「自由度」の値が必要になってくるので、自由度の算出も忘れずに行ってください。
カイ二乗分布を用いて考える場合には、今回求めたカイ二乗値10.21が、自由度1の有意水準5%でのカイ二乗値3.84よりも大きい値を取っているため、帰無仮説が棄却され、「甘いものの好き嫌いと性別には関連がある」という結論になります。
カイ二乗検定の注意点
カイ二乗検定を行ううえで注意すべき点があります。
分割表を作成した際に、期待値が5未満となるセルが分割表のセル全体の20%を上回る場合には、カイ二乗検定の検定統計量がずれる可能性が高いと言われています。
検定統計量がずれれば間違った結果が算出され、結果の解釈も異なってしまう可能性があり、信頼できる結果が出せなくなってしまいます。
そこで、このような場面ではカイ二乗検定とは異なる「Fisherの正確検定」を用いることが推奨されています。
今回は詳しく紹介しませんが、Fisherの正確検定もカイ二乗検定と同様にカテゴリカルデータの解析手法であり、より正確に確率の計算をして変数同士の関連を調べる方法となっています。
自分で分割表を作成したり、解析ツールを用いて解析を行う際には、期待度数が5未満のセルがあるかどうか注意して見るようにしましょう!
カイ二乗検定とは
2つの出来事に関連性があるのかどうかを調べます。
帰無仮説と対立仮説をたて、帰無仮説が起こる確率を計算します。
帰無仮説が起こる確率により、2つの出来事に関連性があるかどうかを調べます。
Excelでカイ二乗検定を行う方法
実測値と期待値を使用して、カイ二乗検定を行います。
例として、虫が好きか嫌いかという結果に性別が関連しているかどうかを調べます。
まずはそれぞれの期待値を求めます。
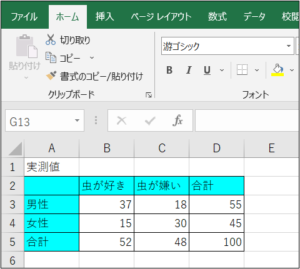
①男性で虫が好きな方の期待値を計算します。
B9のセルに、「=B5*D3/D5」と入力し、Enterキーを押します。
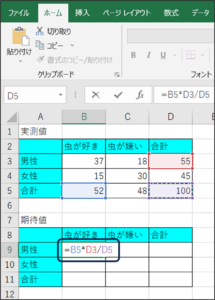
②男性で虫が嫌いな方の期待値を計算します。
C9のセルに、「=C5*D3/D5」と入力し、Enterキーを押します。
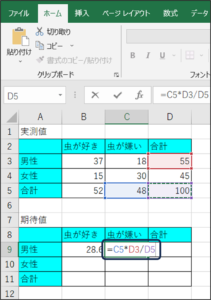
③女性で虫が好きな方の期待値を計算します。
B10のセルに、「=B5*D4/D5」と入力し、Enterキーを押します。
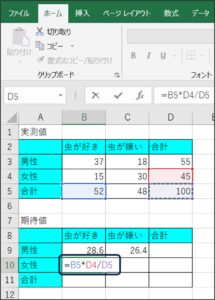
④女性で虫が嫌いな方の期待値を計算します。
C10のセルに、「=C5*D4/D5」と入力し、Enterキーを押します。
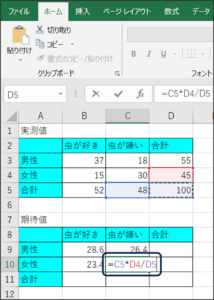
⑤虫が好きな方の合計を求めます。
B11のセルに、「=SUM(B9:B10)」と入力し、Enterキーを押します。
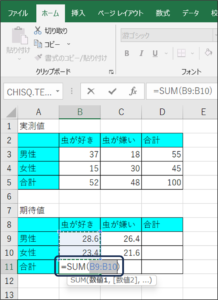
⑥虫が嫌いな方の合計を求めます。
C11のセルに、「=SUM(C9:C10)」と入力し、Enterキーを押します。
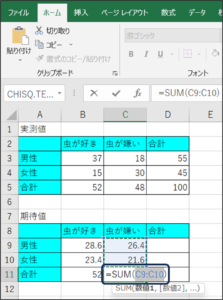
⑦男性の合計を求めます。
D9のセルに、「=SUM(B9:C9)」と入力し、Enterキーを押します。
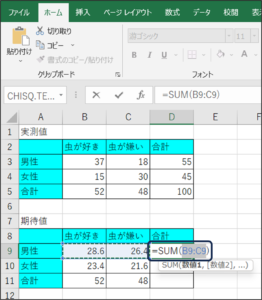
⑧女性の合計を求めます。
D10のセルに、「=SUM(B10:C10)」と入力し、Enterキーを押します。
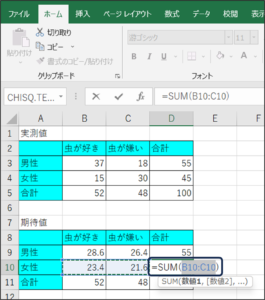
⑨総合計を求めます。
D11のセルに、「=SUM(D9:D10)」と入力し、Enterキーを押します。
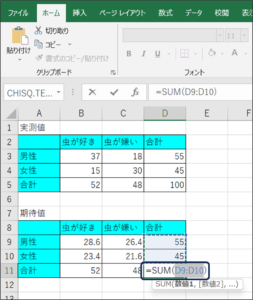
ここから帰無仮説が起こる確率を求めるために使用されるExcel関数である「CHISQ.TEST」を使用する3つの方法を説明します。
セルに直接、関数を手入力する方法
1つ目の方法は、セルに直接、関数を手入力する方法です。
①セルにカーソルがある状態で、「=chi」と入力すると、CHIから始まる関数の一覧がプルダウンで表示されます。
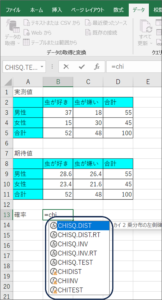
②下矢印で「CHISQ.TEST」までフォーカスを移動させ、Tabキーを押します。
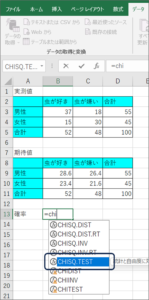
③CHISQ.TEST関数で計算したいデータの入力待ち状態となります。
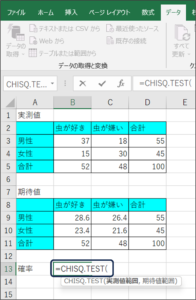
④セルの範囲選択を使用して、実測値のデータを入力します。

⑤データを区切るため、「,」を入力します。
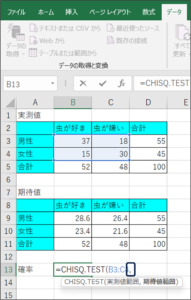
⑥セルの範囲選択を使用して、期待値のデータを入力し、Enterキーを押します。
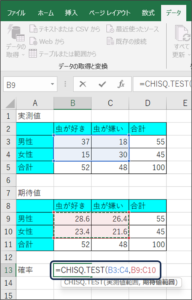
⑦帰無仮説が起こる確率が表示されます。
関数を挿入する方法
2つ目の方法は、関数を挿入する方法です。
①セルが選択されている状態で、fxボタンをクリックします。
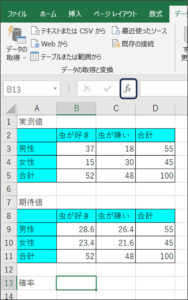
②関数の挿入画面が表示されます。
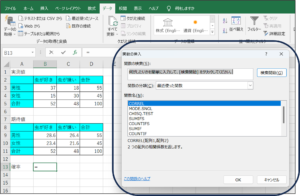
③関数の検索欄に、「CHI」と入力し、検索開始(G)ボタンをクリックします。
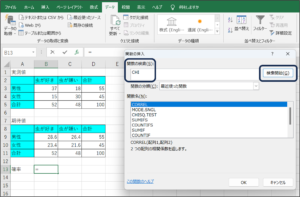
④検索結果の関数名からTEST関数を選択し、OKボタンをクリックします。
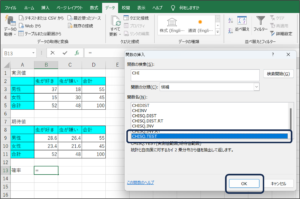
⑤関数の引数画面が表示されます。
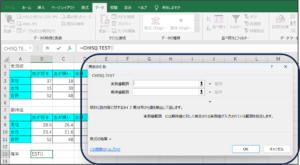
⑥実測値範囲にセルの範囲選択を使用して、実測値のデータを入力します。
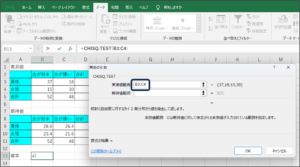
⑦期待値範囲に期待値のデータを入力するため、範囲選択ボタンをクリックします。
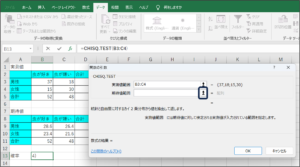
⑧セルの範囲選択を使用して、期待値のデータを入力後、範囲選択ボタンをクリックします。
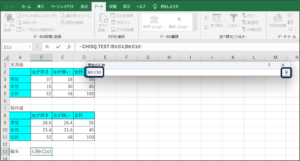
⑨OKボタンをクリックします。
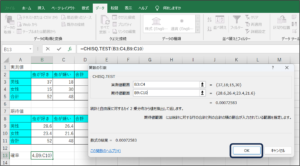
⑩帰無仮説が起こる確率が表示されます。
数式タブから関数を入力する方法
3つ目の方法は、数式タブから関数を入力する方法です。
①セルが選択されている状態で、数式タブのその他の関数の中にある統計のTEST関数を選択します。

②関数の引数画面が表示されます。
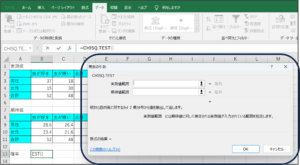
③実測値範囲にセルの範囲選択を使用して、実測値のデータを入力します。
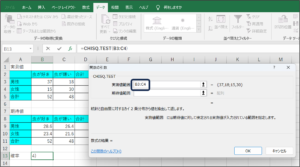
④期待値範囲に期待値のデータを入力するため、範囲選択ボタンをクリックします。
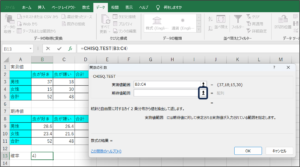
⑤セルの範囲選択を使用して、期待値のデータを入力後、範囲選択ボタンをクリックします。
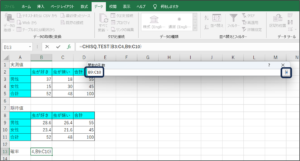
⑥OKボタンをクリックします。

⑦帰無仮説が起こる確率が表示されます。
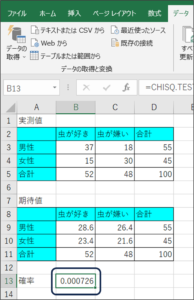
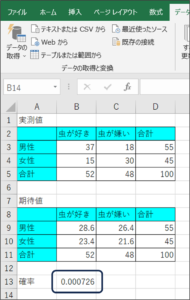
以上の3つの方法で、CHISQ.TEST関数による帰無仮説が起こる確率を求めることができます。
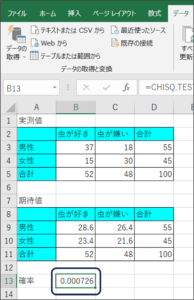
帰無仮説が起こる確率は「0.000726」です。
0.05以下であれば、帰無仮説で仮定した事象はめったに起こらないといわれています。
今回の結果は、0.05以下であるため、「虫が好きか嫌いかという結果に性別が関連していない」という事象が起こる確率は低いということになり、結論としては、「虫が好きか嫌いかという結果に性別が関連する」ということになります。
まとめ
今回は「カイ二乗検定」について、2つの変数の関連を調べる独立性の検定を中心に解説しました。
独立性の検定以外にもカイ二乗検定が用いられる場面はたくさんあるので、今後も様々な場面で目にすることがあると思います。
しかし、今回紹介したカイ二乗検定の流れや自由度の考え方はどの場面でも当てはまる基本的な知識になるので、ぜひ覚えて使いこなせるようになってみてください!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





