皆さんは多重共線性という言葉を聞いたことがありますか?
多重共線性とは、重回帰分析の際によく発生する現象です。解析結果を正しくないものにしてしまう可能性があります。
多重共線性の存在を知らないと、重回帰分析の解析結果がおかしいことに気づけず、誤った判断を下してしまうことがあります。
ですので、多重共線性は、重回帰分析を使う方は必ず知っておくべき知識といえます。
本記事では、回帰分析のおさらいから入り、多重共線性とは何か?なぜ発生するのか?を解説していきます。
さらに、多重共線性への対処方法も併せて説明します。
多重共線性が発生すると重回帰分析の結果はどうなる?
回帰分析のおさらい
回帰分析とは、目的変数と説明変数の関係を調べて、それぞれの関係を明らかにする手法です。2つの例を見ていきましょう。
1つ目の例は、駅前にあるお店の売上高を目的変数、駅の平均乗降客数を説明変数とし、両者の関係を導き出した例です。
駅の乗降客数が売上高に与える影響を見ています。

回帰分析をすると、「売上高=94.6+0.555×乗降客数」となります。この例では、目的変数に対して説明変数が1種類だけあります。これを単回帰分析と言います。
(情報引用元:https://www.statweb.jp/method/kaiki-bunseki/senkeikaiki-case)
2つ目の例は、上の例に対し、「取扱品目数」という説明変数を追加した例です。
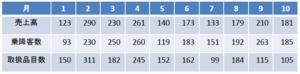
回帰分析の結果、「売上高=0.0937+0.606×乗降客数+0.442×取扱品目数」という回帰式が導き出されました。
このケースでは、目的変数に対し、説明変数が2種類以上あります。これを重回帰分析と言います。
(情報引用元:https://www.statweb.jp/method/kaiki-bunseki/senkeikaiki-jyu-case)
回帰分析では、目的変数を最もよく説明できるように説明変数の係数を求めます。この係数を回帰係数と言います。
係数を求めるには最小二乗法などの方法を使います。なお、回帰分析の詳細な方法は別記事にて説明があります。
多重共線性が起こると回帰分析の結果はどうなるか?
多重共線性とは、説明変数が2つ以上の重回帰分析を行った際に発生することがある現象です。
英語でMulticollinearityといい、略して「マルチコ」と呼ばれることもあります。
多重共線性が発生している場合、求めた回帰係数が直感と真逆の関係(プラスとマイナスが逆)になるなど、適切でない結果が出力されることがあります。
具体的にどのような結果になるか、例を見てみましょう。
この例は、「ビールの出荷数量」を目的変数とし、「気温」、「1年前の出荷数量」を説明変数として重回帰分析した結果です。
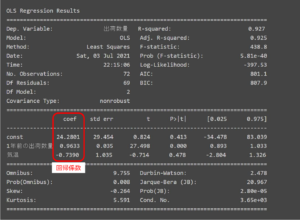
(情報引用元:https://parallelcareerlab.com/?p=1212 図に一部追記)
上図の「coef」と書かれた列が求められた回帰係数となります。
「ビールの出荷数量=24.28+0.9633×1年前の出荷数量-0.7390×気温」という解析結果となっています。
この解析結果は、「気温が1度上昇するとビールの出荷数が0.739ケース減少する」ということを示しています。
しかし、実際は逆であり、気温が上昇するほどビールの出荷数が増えるという傾向があります。
直感的に考えても、暑い夏にビールが売れるようになり、出荷数が増えると考えるのが自然ですよね。
これは、多重共線性が発生しているために発生している現象なのです。
多重共線性を見逃して重回帰分析の結果を受け入れてしまうと、間違えた結論を導き出していることに気づけない可能性があります。
(情報引用元:https://parallelcareerlab.com/?p=996)
多重共線性について
多重共線性とは何か?
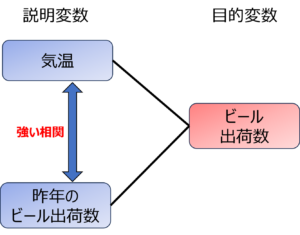
多重共線性とは、説明変数の間に、強い相関を持つ組み合わせが存在していることです。
一方の説明変数が増加すると、それに従って他の説明変数が増加あるいは減少するという傾向が見られる場合、互いに強い相関をもっていると言えます。
上の例では、昨年のビール出荷数と気温の間に強い相関があり、多重共線性が発生しています。
なぜ重回帰分析の結果がおかしくなるのか?
多重共線性が発生している時とは、似たもの同士の説明変数がある場合ともいえます。
このような場合、どちらにどの程度回帰係数を割り当てればよいか分からなくなるため、計算結果が不安定になってしまいます。
その結果、不自然な解析結果が出力されることがあるという認識をもっていただければ大丈夫です。
回帰係数を「取り合っている」というイメージでも良いでしょう。
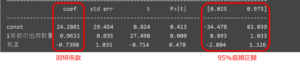
実際に、上の例では、気温の回帰係数の95%信頼区間が-2.804~1.326となっています。
要するに、回帰係数を求めたものの、誤差範囲がとても広くなってしまっているという状態です。
このような場合、サンプルを一つ追加して回帰分析をやり直すと、全く異なる結果となる可能性があります。
最初は気温が上がるとビールの売り上げが下がるという解析結果が出たけど、信頼性を増すためにデータを増やしたら全く逆の傾向が出て頭を抱えてしまう…ということが起こり得ます。
実際のお仕事でこのような事態に陥ったらとても困りますよね。
(表現の参考元:https://xtech.nikkei.com/atcl/learning/lecture/19/00104/00004/?P=3)
どうやって多重共線性に対処するのか?
では、具体的にどのように多重共線性に対処すればよいのでしょうか?
一番大事なことは、重回帰分析の結果を鵜吞みにしないことです。
解析結果を見て、何かがおかしいと気づけなければ、多重共線性を疑うことすらできません。
これまでの経験や直感、ビジネスや研究の知識から結果の妥当性を検証しましょう。
重回帰分析に限らず、データ分析をするときは必ず解析結果が不自然でないか確認するようにしましょう。
解析結果を確認した後、多重共線性が疑われる場合にすべきことは、説明変数どうしの相関係数を確認することです。
そして、不自然な解析結果となった説明変数と強い相関を持つものを見つけ、その中のどれかを除外しましょう。
説明変数を除外したり、また加えたりといった試行錯誤を繰り返して、最も妥当だと思える解析結果を導き出しましょう。
実際のビジネスや研究の場合、明確な「正解」はないことが多いため、粘り強く検証するのが重要です。
ここでは詳しく触れませんが、VIFという指標を使うこともあります。
VIFを参考にしつつ、どの説明変数を残すか検証するのもよいでしょう。
まとめ
多重共線性が重回帰分析に及ぼす影響や対処方法について説明しました。
多重共線性は重回帰分析をする時には避けて通れない問題です。
解析結果を不安定にしてしまうため、気づけなければ大きなミスを犯してしまう可能性があります。
多重共線性に対処するうえで一番大切なのは、重回帰分析の解析結果を鵜呑みにしないことです。
解析結果を疑うことにより、初めて多重共線性に気づくことができます。
これまでの経験や知識から解析結果の妥当性を検証することはデータ分析全般において非常に重要なことです。
このことを忘れずにデータ分析や統計解析に取り組んでいただければ幸いです。





