
今回は「ロジスティック回帰分析」について解説していきたいと思います!
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- 「ロジスティック回帰」とはなにか
- 重回帰分析とロジスティック回帰分析の違い
- 特徴や使い方、結果の解釈など

最後まで楽しんで読んでください!
ロジスティック回帰分析とは?
ロジスティック回帰分析は、ある要因から結果を予測する「回帰分析」の一種で、マーケティングの分野などでもよく使われる解析手法です。
基本的な回帰分析について知りたい方や、一度おさらいしたいという方は「単回帰分析とは Excelでの求め方や活用事例とともに解説」や「重回帰分析とは 活用場面や単回帰分析との違いとともに解説」を読んでみてください!
これからロジスティック回帰分析の特徴について、2つほど紹介していきたいと思います!
目的変数が二値
ロジスティック回帰分析の一番の特徴は「目的変数が二値」であることです。
基本的な回帰分析の一種である「単回帰分析」や「重回帰分析」は、予測したい変数にあたる「目的変数」が身長や売上金額といった連続量になっていました。
しかし、予測したい結果は必ずしも連続量とは限りません。
例えば、受験に合格できるかできないか、顧客はこのサービスに加入するかしないか、病気を発症するかしないかなど、結果が2つのうちのどちらかである場面で予測を行いたい場面も出てくるのではないでしょうか。
そんな時に利用されるのが「ロジスティック回帰分析」です。
求められるのは「判別スコア」
予測したい結果は2種類のどちらかなのですが、実際にロジスティック回帰分析を行って予測される値は「サービスに加入する/加入しない」という2種類ではなく、「サービスに加入する確率」になります。
このような関係式を用いることで「判別スコア」と呼ばれる確率を算出し、サービスに加入する確率を予測していきます。

式を見るととても難しいように思えますが、式自体は覚える必要はないので安心して下さい!
結果の解釈については後ほど解説するので、まずはこの関係式を用いることで「サービスに加入する確率」や「志望校に合格できる確率」を求めることができる、という点をおさえて下さい!
重回帰分析との違いとは?
ここまでロジスティック回帰分析の特徴を紹介してきましたが、「回帰分析」と呼ばれる解析手法はロジスティック回帰分析以外にもたくさんありますよね。
その中でも基本的な手法の1つである「重回帰分析」は、複数の要因から結果を予測する場面で用いられる回帰分析の方法ですが、ロジスティック回帰分析も複数の要因から結果を予測するという状況は一緒では?と思う方もいらっしゃると思います。
重回帰分析とロジスティック回帰分析はどのように使い分ければ良いのでしょうか?
重回帰分析とロジスティック回帰分析の大きな違いは、「目的変数の型」です。
先ほどロジスティック回帰分析の特徴としても紹介しましたが、ロジスティック回帰分析は目的変数が「あり/なし」などで分類できる二値変数の場合に用いられる解析の手法です。
一方で重回帰分析は、目的変数が身長や体重といった連続変数の場合に用いる手法で、複数の要因と結果との関係を直線の式で表すことで結果を予測します。
例えば、身長と体重のデータをプロットした散布図が下の図のようになったとします。
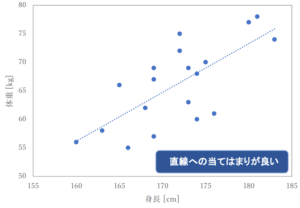
この場合には、2つの変数の関係が直線で表せそうな気がしますよね。
一方で、1日の平均勉強時間と合否の関係を散布図で表した場合はこのようになったとします。

合格を1、不合格を0としてデータをプロットすると、0と1の部分にデータがかたまるので、このような場面で直線を当てはめても正確な予測はできなさそうですよね。
ロジスティック回帰分析は、得られたデータの散布図に対して、下の図のような形の曲線を当てはめて予測をします。
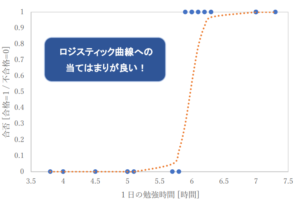
重回帰分析とロジスティック回帰分析では、データに対する直線や曲線の当てはめ方が異なる、ということは是非覚えてください!
ロジスティック回帰分析の使い方・結果の解釈
先程からロジスティック回帰分析を行う場面についていくつか例を挙げていますが、ロジスティック回帰分析も様々な場面で用いることができる、汎用性の高い分析手法です。
マーケティングの分野では、どの年齢層のお客さんが実際に商品を見に来ていて、購入した人はどんな人だったかという顧客情報をデータにまとめてロジスティック回帰分析を行うことで、商品開発などに繋げることができると思います。
医療の分野でも、ある疾患を発症した人と発症していない人の年齢や喫煙の有無などの情報を集めてロジスティック回帰分析を行うことで、ある疾患を発症する確率を予測することができます。
Excelなどでは少し複雑な作業が必要になりますが、統計解析ツールなどを用いることでロジスティック回帰分析を簡単に行うことができます。
実際にロジスティック回帰分析を行うと、単回帰分析や重回帰分析と同様に、それぞれの説明変数に対する回帰係数(βの部分)が算出されますが、解釈も単回帰分析や重回帰分析と同じです。
回帰係数は結果の予測にどの程度影響を与えているのかを表しているので、回帰係数がマイナスの値であれば、予測される確率が下がる方向に影響を与えており、プラスの値であれば、予測される確率が上昇する方向に影響を与えているという解釈ができます。
結果の解釈に重要な「オッズ比」
統計解析ツールなどを用いてロジスティック回帰分析を実施すると、説明変数のそれぞれに対して「オッズ比」という値が算出されていることがあります。
この「オッズ比」は統計学を学ぶ上でも、ロジスティック回帰分析を深く理解する上でも重要な値なので、この記事でも少しだけ紹介します。
オッズ比自体を丁寧に理解しようとすると中々大変ですし、話も少しそれてしまうので、ここでは、ロジスティック回帰分析で算出されるオッズ比が何を表している値なのか、概要を理解して貰えればと思います!
ロジスティック回帰分析で算出されるオッズ比は、それぞれの回帰係数を指数変換した値となっています。

この値は1よりも大きければ、予測される確率が高くなる方向に影響を与えており、1を下回っていれば、予測される確率が低くなる方向に影響を与えています。
例えば、ある生徒が志望校に合格するかを予測するためにロジスティック回帰分析を行ったところ、塾に通っているか/通っていないかという「通塾経験」の変数に対するオッズ比が1.68だった場合、オッズ比が1を上回っているので、塾に通っている場合の方が合格率は高くなる、という解釈ができます。
ただし「合格率が1.68倍」という解釈はできないので、あくまでも予測される確率にどのような影響を与えているのか、という解釈に利用してください!
まとめ
今回は「ロジスティック回帰分析」の特徴や結果の解釈について解説しました。
今後ロジスティック回帰分析を深く理解していくための基本的な部分になりますので、この機会に是非覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





