
今回は、統計調査において重要な考え方の一つである「フィッシャーの三原則」について後ご紹介していきます!
統計検定2級の試験でかなり頻出のテーマですので、是非この機会に学びましょう!
この記事を読むと分かること
- フィッシャーの3原則とは
- 実験計画法との関係
- 系統誤差と偶然誤差
- 繰り返し、ランダム化、局所管理

最後まで楽しんで読んでいただけますと幸いです!
フィッシャーの三原則と実験計画法
実験計画法は、実験を成功させるためのルールのようなもの。
実験には、失敗と成功があります。
たとえば、本来ばらつきがあるのに、ばらつきがないと見誤ったり、
薬(要因)に効果があるのに、ないと見誤ったり、これらは実験の失敗です。
逆に、実験の成功とは、結果を見誤ることなく正しく評価する、効果を検出できるということです。
せっかく実験をするのであれば、正しく結果を評価したいですよね。
そのため、実験を行ううえで、実験計画法のルールは非常に重要なルールだということになります。
そしてこのルールは、R・フィッシャーによって3つの原則に整理されています。
このフィッシャーによって整理された3つの原則が、フィッシャーの3原則(繰り返し、ランダム化、局所管理)なのです。
原則が確立される前は、闇雲に実験をして、上手くいかず、何度もやり直して・・・という風に実験を成功させるために、時間もコストもかかっていました。
それが、このフィッシャーの3原則に則って実験を行えば実験の失敗を防ぐことが出来るようになり、効率的に実験を行えるようになったのです。
フィッシャーの3原則は統計検定2級で頻出のテーマ
フィッシャーの3原則は統計検定2級でよく問われる問題です。
過去問(2014~2019)を見ていくと、2015年11月、2016年11月、2018年6月、2019年6月でフィッシャーの三原則は出題されています。
12回中4回ということで、3回に1回はフィッシャーの3原則が出題されているということになります。
後半の検定問題を少し落としても大丈夫なように、フィッシャーの三原則が出てきたらラッキーだと思って確実に得点にできるよう覚えておくことが大切です。
系統誤差と偶然誤差について
フィッシャーの三原則を理解するうえで大切な誤差について簡単に説明しておきます。
誤差は、系統誤差と偶然誤差という二種類に分けることが出来ます。
それぞれの特長は以下の通り。
- 系統誤差・・・処理の違いによって生まれる誤差のこと。例えば、人や設備、環境などの違いによる誤差は系統誤差になります。偶然ではなく、一定の傾向のある誤差でもあります。(気温が高ければ、定規がごく僅かに長くなる可能性がある、など)
- 偶然誤差・・・たまたま生じる誤差のこと。たとえば、目分量の測定による誤差は偶然誤差だといえます。
フィッシャーの3原則の説明には、系統誤差、偶然誤差という言葉がよく出てきます。
統計検定の問題でも出てくることがあるので覚えておくと便利です。
それぞれの原則の解説
それでは、ここからはそれぞれの原則について細かく見ていきましょう。
フィッシャーの3原則:①繰り返し(replication)
繰り返しは、同じ水準のなかで、独立した実験を繰り返すという原則です。
同じ処理を何度も繰り返して行うことで、偶然誤差の大きさを評価することが出来ます。
(偶然誤差による測定値への影響を減らしていく、ともいえます。)
たとえば、人間を対象とした臨床試験でたった一人から得られたデータに差があったとしても、それが意味のある差だといえるでしょうか。
もしかしたら、そのとき得られたデータの差は、系統誤差による差かもしれませんし、偶然誤差による差かもしれません。
そのためこの場合、人間には個体差があるため、多くの被験者のデータを取ることが必要になります。
たくさんのデータを集めて偶然誤差のばらつきの大きさが分かれば、真の平均の取り得る値が分かります。
そしてその範囲よりも系統誤差が大きければ、臨床試験で得られた差に意味がある(投薬の実験であれば、薬に効果がある)ということになります。
これが繰り返しを行う効果です。
偶然誤差の大きさを評価できるというのがポイントです!
フィッシャーの3原則:②ランダム化(randomization)
ランダム化は、処理をランダムに割り付けることで、制御が困難な要因の影響(系統誤差)を偶然誤差として転化できるという原則です。
ランダム化は、別名「無作為化」とも言います。
例えば、最初に実験するときと、最後に実験するときで、気温や湿度など環境が変わる場合があります。(1日かけて行う実験などで起こりやすいです)
そのほかにも、実験を重ねる中で被験者が実験に慣れることで、実験において良い成績を残しやすくなったりするなどのケースもあります。
これらは先述の系統誤差の一種です。
この系統誤差を取り除くことで、実験の成功につなげることが出来ます。
その方法こそが、ランダム化なのです。
例えば、被験者全員が英語の小テスト①~③を、①→②→③の順番で受けるとします。
そうすると①の点数よりも③の点数の方が、全体的に優れたという差が出たときに、
「それは①を解いたことで被験者が英語の試験に慣れたからそのような結果になった」という風にも考えられます。
そうするとこれは系統誤差になってしまいます。
そこで、これを被験者によって受ける順番をバラバラにしてみます。
Aさんは②→①→③、Bさんは③→②→①、Cさんは①→③→②・・・などのように順番をランダム化します。
そうするすることで、テストの順番による系統誤差を偶然誤差に転化することができ、
小テスト本来の点数について純粋に考えることが出来るようになるのです。
フィッシャーの3原則:③局所管理(local control)
局所管理とは、実験の場をできるだけ均一に保つように管理されたいくつかのブロックに分けて実験を行う原則のことです。
先に挙げた、繰り返しとランダム化はなんとなくイメージがつきやすいと思いますが、
局所管理はなかなか聞き慣れないと思うので具体例を挙げて説明していきます。
例えば、とある農地で、施肥効果を調べるために、日当たりのよい場所と悪い場所のブロックに分けて、日当たり以外の条件はできる限りそろえて以下の流れで実験を行います。
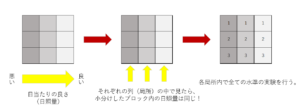
本来は、要因(施肥の効果)だけを見たいのに、そのままでは日当たりという系統誤差が入ってきてしまっています。
そこで、その日当たりという系統誤差自体も一つの要因として扱うことで、系統誤差自体をなくしてしまうというやり方が局所管理です。
一部の系統誤差をブロック間変動(ブロック間誤差)として除去するために用いる原則です。
特に大規模な実験では、系統誤差の影響の軽減に効果的な原則として知られています。
まとめ
今回は、フィッシャーの3原則について詳しく解説していきました。
ランダム化、繰り返し、局所管理のそれぞれの意味と特徴は、統計検定でも問われやすいテーマです。
また、統計調査を行う際にも非常に重要な考え方になってきますので、しっかり覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。







