今回は「t検定」についてご紹介していきます。
仮説検定にはいろいろな種類がありますが、そのなかでもt検定は統計解析で最も頻繁に使われると言っても過言ではない手法です。
検定を学ぶ基本にもなりますので、是非最後まで読んでみてください!
この記事を読むと分かること
- t検定とは
- 具体的なt検定の手順
- t検定の種類と活用事例

是非最後まで楽しんで読んでいただけますと幸いです!
t検定とは
t検定は、平均の差の検定ともいわれる分析手法です。
わかりやすくいうと、2つのグループのデータの平均に、統計的に意味のある差(有意差)があるかどうかを確認したいときに使われます。
具体的には、検定統計量が「t分布」と呼ばれる分布に従うことを利用して行われる検定です。
t分布は「自由度」と呼ばれるデータが自由に取れる数によって分布の形が変わるのですが、自由度が大きくなると正規分布に近づいていくことが知られています。
図にすると、以下のようなイメージです。
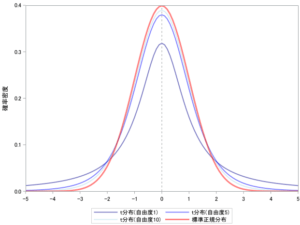
この図からも、自由度が上がっていくとどんどん正規分布に近づいていることが分かります。
このような性質から、t検定は正規分布に従っていることを利用して行われるz検定とも密接な関係にあります。
t検定もz検定も、どちらも母平均に対して明らかにしたいことがある時に用いられる検定方法です。
例えば、ある工場で作られている部品の重さが15gとなっているのか、それとも誤差とは言い切れない範囲で15gより重くなっているのかどうかを、ランダムに取り出した100個のサンプルから評価していく場合などにもt検定を活用することができます。
t検定は、母分散が未知の場合に用いる
t検定は母分散が未知の場合に使う検定手法です。母分散が分かっているときはZ検定をという方法を使います。
先ほどの工場の部品で言えば、部品の重さのばらつきは2gまでとしていることが既に分かっている場合はz検定を行うことができます。

一方でt検定は、母集団の分散が分かっていなくても検定を行うことができる方法です。
工場の部品のように事前に平均と分散が規定されている場合もありますが、一般的に統計解析を行う場合には、母集団の分散が分からないという場面がほとんどなので、実際はz検定よりt検定を行うことの方が多いです。
t検定の種類
t検定は、先ほど紹介したような母分散が分からない場面での母平均に対する検定だけではなく、様々な場面で活用できる非常に汎用性の高い検定です。
ここからはt検定の種類について、どのような場面で使われるのか具体例とともにいくつか紹介していきたいと思います。
1標本t検定
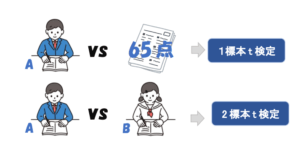
1標本のt検定は、先ほど紹介した工場の部品の例と同様で、得られたデータからある1つの値である母平均と等しいかどうかを検定するものです。
1つの標本から得られた情報をもとに母平均との比較を行うので「1標本」のt検定と呼ばれます。
2標本t検定(対応あり、対応なし)
上の説明を読んで気づいた方もいるかもしれませんが、2標本t検定は2つの標本から得られる情報を用いて、2つの集団の平均に差があるかどうかを検定するものです。
例えば、Aクラスの英語の平均点とBクラスの英語の平均点に差があるかどうかを検定する場合には、2標本t検定を利用します。
「英語の平均点が65点かどうか」など、特定の値に対して検定をするわけではないので、先ほどの1標本t検定は使えないということが分かるかと思います。
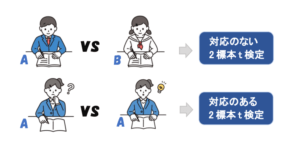
また、2標本t検定には「対応のないt検定」と「対応のあるt検定」の2種類があります。
この2つの検定方法の違いは、簡単に言うと「同一人物での比較をしているかどうか」の違いになります。
先ほどの英語の点数の例で言うと、AクラスとBクラスでは同一人物がいない中で平均点を比較することになるので「対応のないt検定」となります。
一方で、Aクラスの中で2回英語のテストを実施して、1回目と2回目の平均点に差があるかどうかを検定したい場合には、同じAクラスの生徒の平均点を比較することになるので「対応のあるt検定」となります。
Welchのt検定
実は、対応のない2標本のt検定にはさらに細かい種類が存在しています。
対応のない2標本のt検定では、2つの集団の分散が等しいという前提のもと検定を行っています。
しかし、2つの集団の分散が等しいということを仮定して考えても、標本の分散に大きな差があり、仮定するのが難しい場面も出てきます。
2つの集団の分散が等しいと仮定できないと判断された場合には「welchのt検定」という方法を用います。(ここでは詳細は割愛します)
少し複雑になってきたので、t検定の種類についてフローチャートにしてみると、以下のようなイメージです。
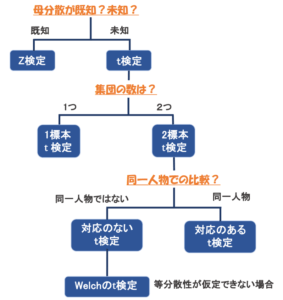
比較したいものやどのような集団と比較しているかによって、同じt検定でも異なる検定統計量を使うことになるので、状況をよく考えて使う必要があるというのを覚えておきましょう。
t検定の手順
それでは実際にt検定の手順について紹介していきたいと思います。
仮説検定全般の手順やz検定については「仮説検定とは 推定との違いや活用事例とともに解説」の記事でも詳しく紹介しているので、おさらいをしたい方はそちらの記事も読んでみてください!
まずは、t検定を行う手順を大まかにまとめたいと思います。
➀ 帰無仮説・対立仮説を立てる
➁ 有意水準を設定する
➂ 検定統計量であるt値を求める
➃ t分布表などを用いてp値を求める
➄ p値と有意水準を比較して有意差を判定
➀と➁はどの仮説検定でも同じ手順を踏みますが、➂の検定統計量の計算はz検定とは異なります。
t検定の検定統計量は「t値」と呼ばれます。
先ほど紹介した部品の例のように、母分散が分からない場面で母平均に対する検定を行う場合には、以下の式によって求めることができます。
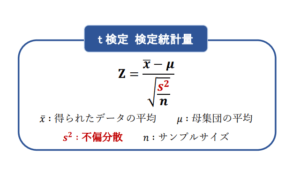
z検定の検定統計量と似たような式となっていますが、母分散にあたる部分が「不偏分散」に代わっています。
t検定は母分散が分からない場面での検定なので、母分散の代わりに得られたデータから求めた不偏分散を利用しています。
不偏分散は以下の式で求めることができますが、通常分散を求める時にnで割る部分をn-1で割るというだけの違いなので、ぜひ覚えて欲しい式です。

このようにして求められたt値は、自由度n-1のt分布に従います。
このことを用いて、④にあたるp値を求めていくことになります。
p値は、t分布表などを用いることでも求めることができますが、Excelなどのツールを使っても簡単に求めることができます。
Excelでt検定を行う方法
ここからは、Excelでt検定を行う方法を解説します。
Excelの関数であるT.TEST関数を使用してt検定を行います。
これからT.TEST関数を使用して検定する3つの方法を説明します。
セルに直接、関数を手入力する方法
1つ目の方法は、セルに直接、関数を手入力する方法です。
例として、運動前と運動後の体重の平均に差があるかどうかについて、同じグループによるt検定で検定する方法を説明します。
- 帰無仮説:運動前と運動後の体重の平均に差はない
- 対立仮説:運動前と運動後の体重の平均に差はある
①セルにカーソルがある状態で、「=t」と入力すると、Tから始まる関数の一覧がプルダウンで表示されます。
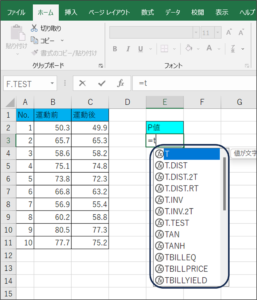
②下矢印で「TEST」までフォーカスを移動させ、Tabキーを押します。
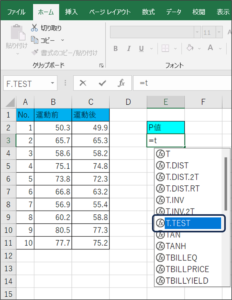
③TEST関数で比較するデータの入力待ち状態となります。
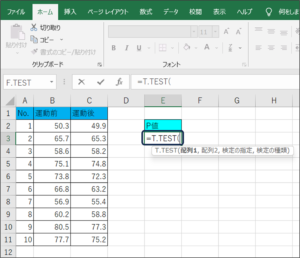
④セルの範囲選択を使用して、運動前の体重データを入力します。
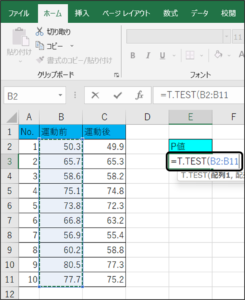
⑤データを区切るため、「,」を入力します。
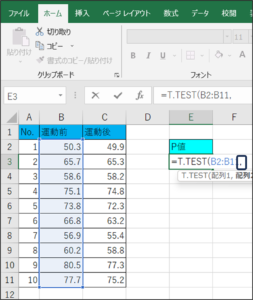
⑥セルの範囲選択を使用して、運動後の体重データを入力します。
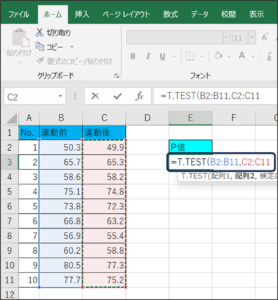
⑦データを区切るため、「,」を入力します。
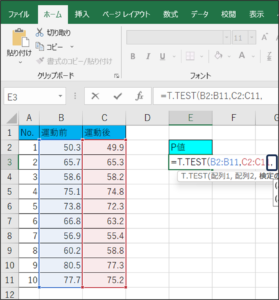
⑧検定の指定を行います。
「1」は片側検定、「2」は両側検定です。
今回は、差があるかどうかを求めるため、「2」を入力します。
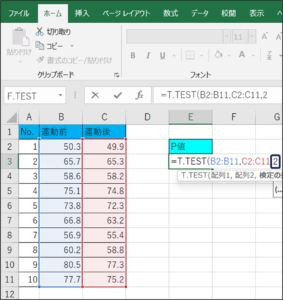
⑨データを区切るため、「,」を入力します。
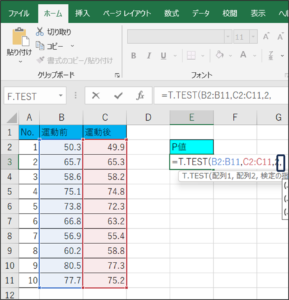
⑩検定の種類を選択します。
「1」は同じグループによるt検定、「2」は違うグループで分散が等しいサンプルによるt検定、「3」は違うグループで分散が異なるサンプルによるt検定(Welch法)です。
今回は、同じグループによるt検定のため、「1」を入力し、Enterを押します。
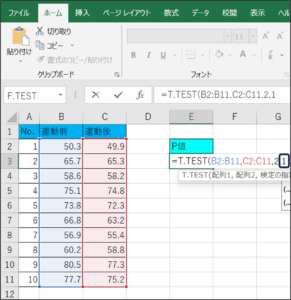
⑪t検定で判断に使用するP値が表示されます。
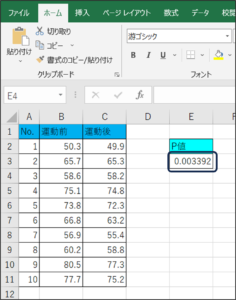
P値は「0.003392」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以下であるため、「運動前と運動後の体重の平均に差はない」と考えられます。
関数を挿入する方法
2つ目の方法は、関数を挿入する方法です。
例として、ある商品の性別による購入金額の平均に差があるかどうかについて、違うグループで分散が等しいサンプルによるt検定で検定する方法を説明します。
- 帰無仮説:性別による購入金額の平均に差はない
- 対立仮説:性別による購入金額の平均に差はある
①セルが選択されている状態で、fxボタンをクリックします。
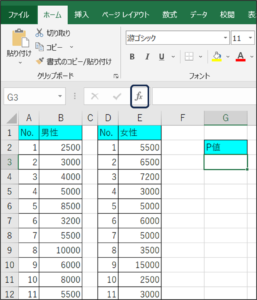
②関数の挿入画面が表示されます。
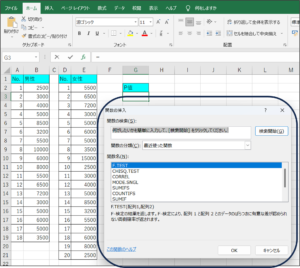
③関数の検索欄に、「T」と入力し、検索開始(G)ボタンをクリックします。
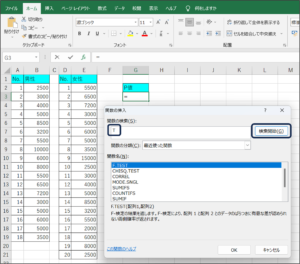
④検索結果の関数名からTEST関数を選択し、OKボタンをクリックします。
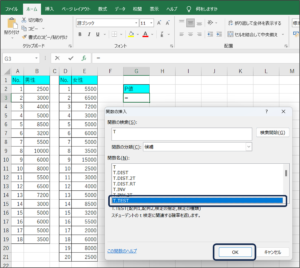
⑤関数の引数画面が表示されます。
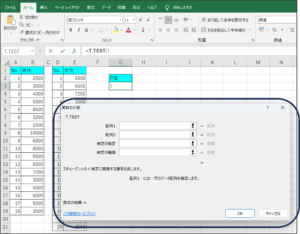
⑥配列1にセルの範囲選択を使用して、男性の購入金額のデータを入力します。
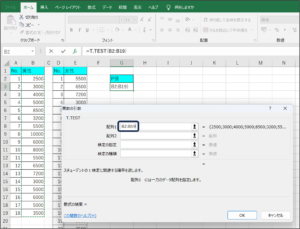
⑦配列2に女性の購入金額のデータを入力するため、範囲選択ボタンをクリックします。
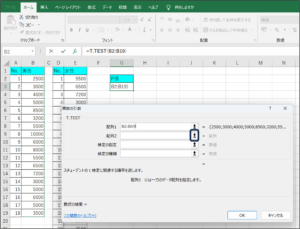
⑧セルの範囲選択を使用して、女性の購入金額のデータを入力後、範囲選択ボタンをクリックします。
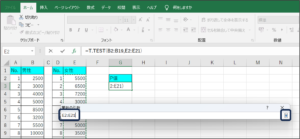
⑨検定の指定を行います。
「1」は片側検定、「2」は両側検定です。
今回は、差があるかどうかを求めるため、「2」を入力します。
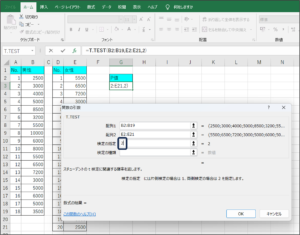
⑨検定の種類を選択します。
「1」は同じグループによるt検定、「2」は違うグループで分散が等しいサンプルによるt検定、「3」は違うグループで分散が異なるサンプルによるt検定(Welch法)です。
今回は、違うグループで分散が等しいサンプルによるt検定のため、「2」を入力し、Enterを押します。
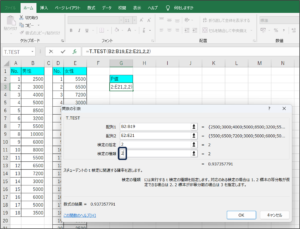
⑩t検定で判断に使用するP値が表示されます。
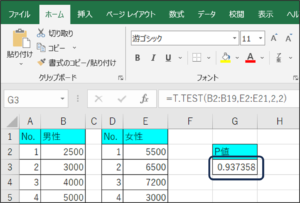
P値は「0.937358」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以上であるため、「性別による購入金額の平均に差はある」と考えられます。
数式タブから関数を入力する方法
3つ目の方法は、数式タブから関数を入力する方法です。
例として、ある商品の性別による購入金額の平均に差があるかどうかについて、違うグループで分散が異なるサンプルによるt検定(Welch法)で検定する方法を説明します。
- 帰無仮説:性別による購入金額の平均に差はない
- 対立仮説:性別による購入金額の平均に差はある
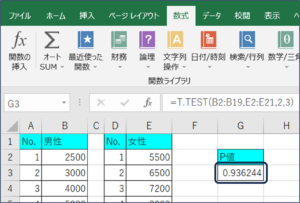
①セルが選択されている状態で、数式タブのその他の関数の中にある統計のTEST関数を選択します。
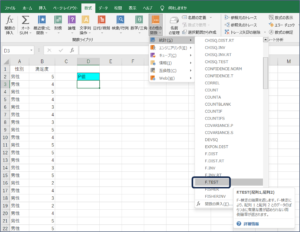
②関数の引数画面が表示されます。
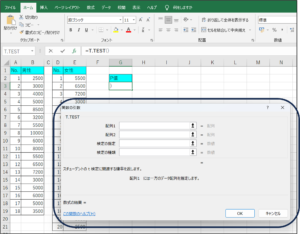
③配列1にセルの範囲選択を使用して、男性の購入金額データを入力します。
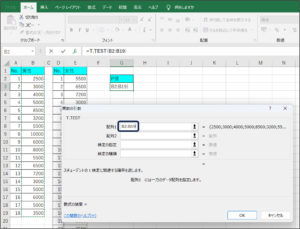
④配列2に女性の購入金額データを入力するため、範囲選択ボタンをクリックします。
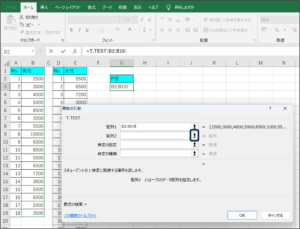
⑤セルの範囲選択を使用して、女性の購入金額データを入力後、範囲選択ボタンをクリックします。
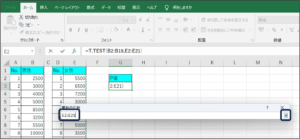
⑥検定の指定を行います。
「1」は片側検定、「2」は両側検定です。
今回は、差があるかどうかを求めるため、「2」を入力します。
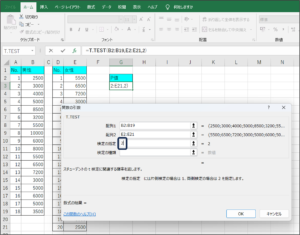
⑦検定の種類を選択します。
「1」は同じグループによるt検定、「2」は違うグループで分散が等しいサンプルによるt検定、「3」は違うグループで分散が異なるサンプルによるt検定(Welch法)です。
今回は、違うグループで分散が等しいサンプルによるt検定(Welch法)のため、「3」を入力し、Enterを押します。
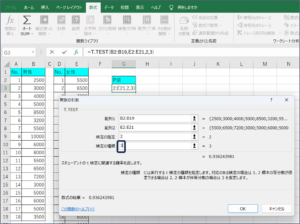
⑧t検定で判断に使用するP値が表示されます。
P値は「0.936244」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以上であるため、「性別による購入金額の平均に差はある」と考えられます。
Excelの分析ツールを使用して、t検定を行う方法
次に、Excelの分析ツールを使用して、t検定を行う方法を説明します。
Excelの分析ツールを使用して、t検定を行います。
分析ツールを使用する前に、Excelの分析ツールが使用できるように設定します。
①Excelを起動し、オプションをクリックします。

②アドインを選択して、管理(A):に「Excel アドイン」を設定し、設定(G) ...ボタンをクリックします。
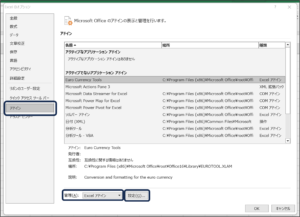
③アドイン画面が表示されますので、分析ツールにチェックをつけ、OKボタンをクリックします。
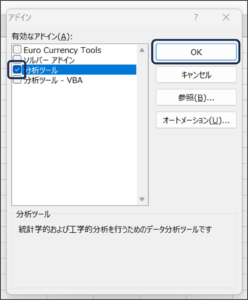
④データタブをクリックし、データ分析が追加されていることを確認します。
データ分析が追加されていれば、データ分析ツールの準備は完了です。

Excelの分析ツールを使用した前述の3つのt検定の方法を説明します。
例として、運動前と運動後の体重の平均に差があるかどうかについて、同じグループによるt検定で検定する方法を説明します。
- 帰無仮説:運動前と運動後の体重の平均に差はない
- 対立仮説:運動前と運動後の体重の平均に差はある
①データタブからデータ分析をクリックします。
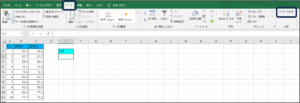
②データ分析画面が表示されますので、「t検定: 一対の標本による平均の検定」を選択し、OKボタンをクリックします。
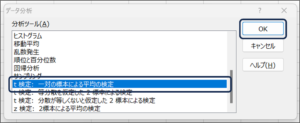
③t検定: 一対の標本による平均の検定画面が表示されます。
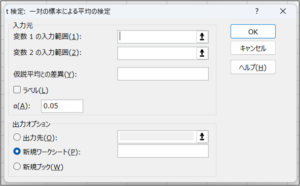
| 項目名 | 説明 |
| 変数1の入力範囲(1) | 比較するデータを範囲選択します。 |
| 変数2の入力範囲(2) | 比較するデータを範囲選択します。 |
| 仮説平均との差異(Y) | 2群の平均値にある特定の差を仮定する際に設定します。 |
| ラベル(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。 |
| α(A) | 有意水準を指定します。初期値は、「0.05」です。 |
| 出力先(O) | 同じシート内に検定結果を出力する場合に、チェックを入れます。 検定結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 検定結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 検定結果を新しいブックに出力する場合に、チェックを入れます。 |
④変数1の入力範囲にセルの範囲選択を使用して、運動前の体重データを入力します。
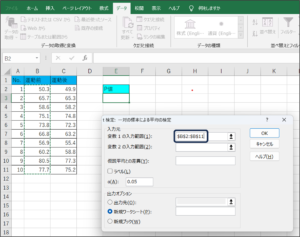
⑤変数2の入力範囲に運動後の体重データを入力するため、範囲選択ボタンをクリックします。
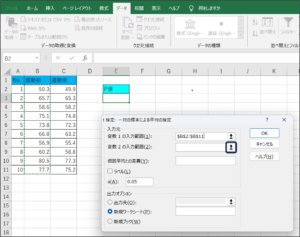
⑥セルの範囲選択を使用して、運動後の体重データを入力後、範囲選択ボタンをクリックします。
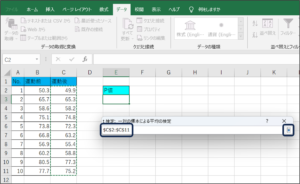
⑦条件を設定して、OKボタンをクリックします。
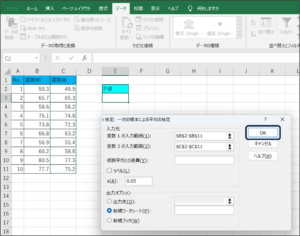
⑧t検定で判断に使用するP値が表示されます。
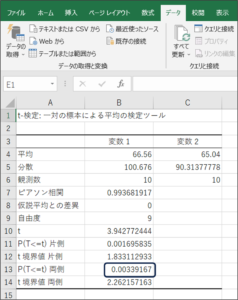
P値は「0.00339167」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以下であるため、「運動前と運動後の体重の平均に差はない」と考えられます。
例として、ある商品の性別による購入金額の平均に差があるかどうかについて、違うグループで分散が等しいサンプルによるt検定で検定する方法を説明します。
- 帰無仮説:性別による購入金額の平均に差はない
- 対立仮説:性別による購入金額の平均に差はある
①データタブからデータ分析をクリックします。
②データ分析画面が表示されますので、「t検定: 等分散を仮定した2標本による検定」を選択し、OKボタンをクリックします。
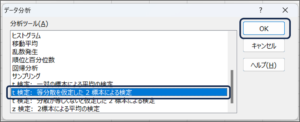
③t検定: 等分散を仮定した2標本による検定画面が表示されます。
| 項目名 | 説明 |
| 変数1の入力範囲(1) | 比較するデータを範囲選択します。 |
| 変数2の入力範囲(2) | 比較するデータを範囲選択します。 |
| 仮説平均との差異(Y) | 2群の平均値にある特定の差を仮定する際に設定します。 |
| ラベル(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。 |
| α(A) | 有意水準を指定します。初期値は、「0.05」です。 |
| 出力先(O) | 同じシート内に検定結果を出力する場合に、チェックを入れます。 検定結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 検定結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 検定結果を新しいブックに出力する場合に、チェックを入れます。 |
④変数1の入力範囲にセルの範囲選択を使用して、男性の購入金額データを入力します。
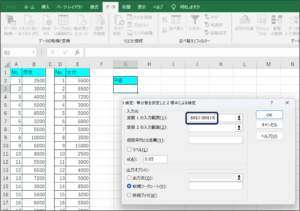
⑤変数2の入力範囲に女性の購入金額データを入力するため、範囲選択ボタンをクリックします。
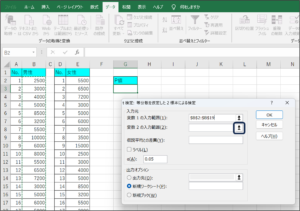
⑥セルの範囲選択を使用して、女性の購入金額データを入力後、範囲選択ボタンをクリックします。
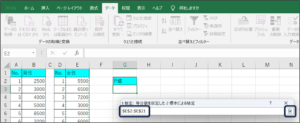
⑦条件を設定して、OKボタンをクリックします。
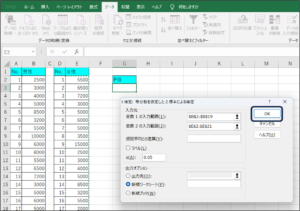
⑧t検定で判断に使用するP値が表示されます。
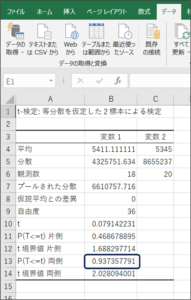
P値は「0.937357791」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以上であるため、「性別による購入金額の平均に差はある」と考えられます。
例として、ある商品の性別による購入金額の平均に差があるかどうかについて、違うグループで分散が異なるサンプルによるt検定(Welch法)で検定する方法を説明します。
帰無仮説:性別による購入金額の平均に差はない
対立仮説:性別による購入金額の平均に差はある
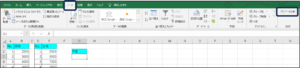
①データタブからデータ分析をクリックします。
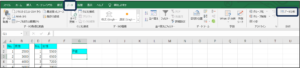
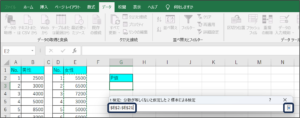
②データ分析画面が表示されますので、「t検定: 分散が等しくないと仮定した2標本による検定」を選択し、OKボタンをクリックします。
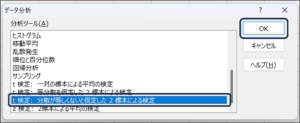
③t検定: 分散が等しくないと仮定した2標本による検定画面が表示されます。
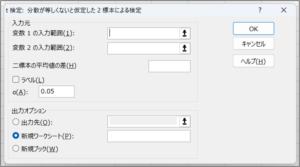
| 項目名 | 説明 |
| 変数1の入力範囲(1) | 比較するデータを範囲選択します。 |
| 変数2の入力範囲(2) | 比較するデータを範囲選択します。 |
| 二標本の平均値の差(H) | 2群の平均値にある特定の差を仮定する際に設定します。 |
| ラベル(L) | データの範囲を選択した際、先頭行の項目名も範囲選択した場合に、チェックを入れます。 チェックを入れ忘れた場合は、以下のようなエラーメッセージが表示されます。 |
| α(A) | 有意水準を指定します。初期値は、「0.05」です。 |
| 出力先(O) | 同じシート内に検定結果を出力する場合に、チェックを入れます。 検定結果を出力する先頭行のセルを指定します。 |
| 新規ワークシート(P) | 検定結果を新しいワークシートに出力する場合に、チェックを入れます。 |
| 新規ブック(W) | 検定結果を新しいブックに出力する場合に、チェックを入れます。 |
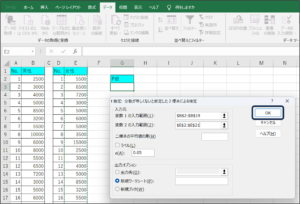
④変数1の入力範囲にセルの範囲選択を使用して、男性の購入金額データを入力します。
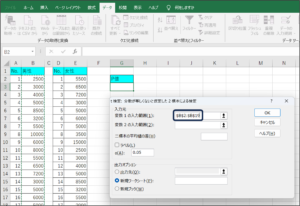
⑤変数2の入力範囲に女性の購入金額データを入力するため、範囲選択ボタンをクリックします。
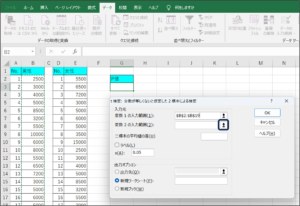
⑥セルの範囲選択を使用して、女性の購入金額データを入力後、範囲選択ボタンをクリックします。
⑦条件を設定して、OKボタンをクリックします。
⑧t検定で判断に使用するP値が表示されます。
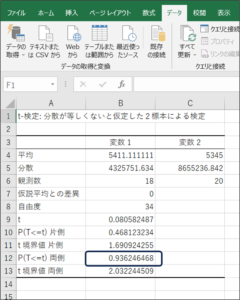
P値は「0.936246468」です。
P値が0.05以下であれば、平均に差がないといわれています。
今回の結果は、0.05以上であるため、「性別による購入金額の平均に差はある」と考えられます。
以上で、Excelの分析ツールを使用した説明は終わりです。
まとめ
今回は、汎用性の高い検定の1つであるt検定について、ご紹介しました。
検定の目的は何か、既に分かっている情報は何か、などを丁寧に確認しながらt検定を使いこなせるようになると、統計学の理解も深まっていきます。
気になった方は、統計検定などの実践問題を通してt検定について学んでみてください。