製造業では、製品の品質を管理するために統計学を活用しています。
日々大量生産されている製品に対し、統計学を活用してその状態を把握し、品質の維持・改善、すなわち品質管理に役立てています。
当記事では、統計学が製品の品質管理に役立つ理由、統計学を品質管理に活用する方法を解説していきます。
統計学と品質管理の関係について理解を深めていただければ幸いです!
品質管理について
製造業における品質管理とは?
自社が生産する製品が顧客の要求する以上の品質を備えていることを保証するための活動です。
英語表記のQuality Controlの頭文字をとり、「QC」と略されることもあります。
具体的な活動としては、工程管理活動・品質改善活動の2つが挙げられます。
・工程管理活動
材料、設備、人、作業方法、測定といった製品の品質に影響を及ぼす要因を管理する活動のことです。
製品の製造に携わる人を教育したり、設備を定期的に点検したりすることが挙げられます。
なお、これら5つの要因は英語表記の頭文字がすべてMなので、まとめて「5M」と呼ばれることが多いです。
環境(温度、湿度など)という要因も含め、「5M+1E」と呼ばれることもあります。
・品質改善活動
製品に品質問題が発生した際、原因を追究し、再発・未然防止につなげる活動のことです。
前述の5M+1Eの観点で問題の真因を追究し、再び問題が起こらないように仕組みの改善を行います。
なぜ品質管理をする必要があるのか?
品質管理を行うことにより得られるメリットとして、次の2つが挙げられます。
顧客の信頼獲得
品質の高い製品を安定して納入することにより、顧客から信頼を得ることができます。
逆に、品質の低い製品、すなわち不良品ばかりを顧客に納入した場合はどうなるでしょう?
当然、顧客からは信用されなくなり、最悪の場合は製品を発注してくれなくなるということもあり得ます。
品質管理は、顧客からの信頼と自社の売り上げを守るために欠かせない活動です。
自社製品のブランド力向上
製品の品質を高いレベルで維持することは、自社製品のブランド力向上に繋がります。
品質の高い製品を安定して作り続けることができれば、「●●社の製品は丈夫だ、壊れにくい」といったポジティブな評判が広まることもあり得ます。
これによりブランド力が向上し、顧客に選ばれる製品となるでしょう。
品質管理とは、顧客の信頼を勝ち取り、自社の売り上げを守るために欠かせない活動なのです。
統計学を品質管理に活用するメリット
統計学を品質管理に活用することにより、少数のサンプルから量産品全体の姿を推測することができます。
製造業では、毎日大量の製品を生産しています。例えば、トヨタ自動車では毎日約10,000台以上の車を生産しています[1]。
製品の品質を保証するためには、すべての製品を検査し、品質に問題のないことを確認するのが理想でしょう。
ですが、1日に10,000個以上の製品を全て検査するのはコストや時間の観点で現実的ではありません。そこで登場するのが統計学です。
下図[2]のように、統計学を用いれば、一部のサンプルを抜きとって検査することにより、量産品全体の品質を予測することが可能になります。
「抜きとった一部のサンプルから全体を推測する」という考え方は製造業以外でも幅広く使用されています。
例えば家計調査などが挙げられます。
統計学を品質管理に活用するための方法
工程抜き取りデータを用いた不良率予測
抜き取ったサンプルデータから全体の不良率を予測した例を挙げます。
例えば、工程から製品を20個抜き取って重さを測定したところ、以下のような測定値が得られました。
なお、重量が22±3gの範囲内に入っていればOKとします。
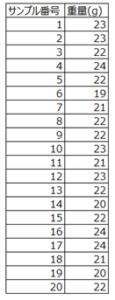
(デ―タ参照元[2])
測定値をヒストグラムで可視化すると下図のようになります。なお、ヒストグラムとは、データをいくつかの区間に分け、その区間に入っているデータの個数を棒グラフのようなかたちで表した図のことです。
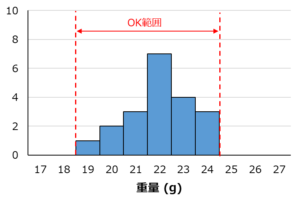
測定値はすべて22±3gの範囲内に入っていますので、「この工程は品質の高い製品を作ることができる」と判断してしまうかもしれません
しかし、「今回抜き取った20個の製品重量が偶然22±3gに入っていただけで、数を増やしていけば範囲から外れる製品も出てくるのでは?」と考えた読者の方もいらっしゃるかもしれません。
統計学を用いるとこの疑問を解消することができます。
工程で生産される全製品の重量分布を下図オレンジ色曲線のように推測することができます。
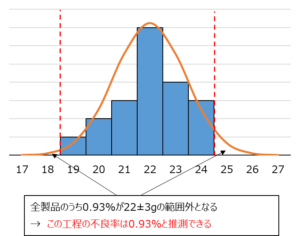
このように、ヒストグラムがおよそ左右対称の形を示している時、測定値は「正規分布」と呼ばれる山型の分布に従っていると仮定することができます。
そして、この場合、この「正規分布」が生産されるすべての製品の重量分布なのです。
この正規分布のグラフを見ると、一部が22±3gからはみ出ている、すなわち不良品であることが分かります。
詳細な計算過程は省きますが、製品全体のうち0.93%が不良品であるということも計算できます。
「正規分布」という統計学の考え方を用いることにより、抜き取ったサンプルから量産品全体の不良率を予測することが可能になります。
ヒストグラムを用いた工程状態の把握
先ほどの例で紹介したヒストグラムはおよそ左右対称の形を示していました。
このような左右対称のヒストグラムを「一般形のヒストグラム」といいます。
しかし、実際にヒストグラムを作成すると、一般形でない形を示すこともあります。以下に2つの例を示します。
ふた山型
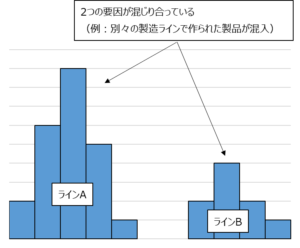
2つの要因が交じり合っている可能性があります。
異なるロットの原料を使用していた、別のラインで作った製品のデータが混ざっていたなどの原因が考えられます。
この場合は、元のデータを原料ロット、ラインごとに層別してヒストグラムを作成しなおしましょう。
絶壁型
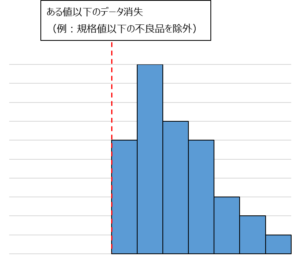
一般系と比較すると、ある値を境にデータがばっさり削除されていることが分かります。
製品を全て検査し、不良品を除外している場合などによく現れます。また、測定方法に何らかの異常がある場合もあります。
このように、データをとってヒストグラムを作成すると、工程の異常発見につなげることができます。
また、工程について知識のある方であれば、原因をある程度推測することができます。
そこから、先ほど紹介した5Mに異常がないかという観点で改善につなげることも可能です。
ヒストグラムは工程の状態の把握・改善に役立つツールです。
まとめ
ここまで、統計学と品質管理の関係について説明してきました。品質管理とは企業を存続させるために欠かすことのできない活動です。
製造業では製品を日々大量に生産していますが、製品全体の品質を効率よく予測するために統計学を活用しています。
また、ヒストグラムを用いることにより、工程の状態を把握し、異常があった場合は改善につなげることができます。
製造業において、製品の品質を把握し、維持・改善するために統計学は必要不可欠なものです。
【出典】
[1] https://global.toyota/jp/kids/faq/production/002.html
[2] https://urban-cafeteria.com/normaldistributiondrawing.html





