
こんにちは!統計ブロガーのにっしーです!
統計学を勉強していると、“○○の分布は正規分布に従う”などといった言葉をよく聞くと思います。
では、正規分布とは一体どんな形で、どんな特徴を持つ分布なのでしょうか。
今回は「正規分布は一体何を表しているのか分からない…」と感じている方に向けて、絶対に押さえておきたい正規分布の基本的な性質と身近な例を3つずつご紹介します!
この記事を読むと、以下のことが分かるようになります!
この記事を読むと分かること
- 正規分布とは
- 日常に潜む正規分布の例

是非最後まで楽しんで読んでいただけますと幸いです!
正規分布とは
まずはじめに正規分布を表す関数の式を示します。
f(x)=1/√2πσ e^(-(x-μ)^2/(2σ^2 ))
パッと見ただけでもとても複雑な式ですよね。
この式を見るだけで逃げたくなってしまう方もいるかもしれませんが、ここではこの式の意味を完全に理解する必要はないので安心してください!
正規分布は別名ガウス分布とも呼ばれ、統計学の中で最も重要であるといっても過言ではない基本的な確率分布です。
先ほど示した正規分布を表す式の変数のうち、平均μと標準偏差σ(分散σ^2)を決めることで、正規分布を描くことができるようになります。
ここからは、正規分布の基本的な性質を3つ紹介していきたいと思います。
これだけは押さえておきたい!正規分布の基本性質
1. 左右対称な釣鐘型の分布
正規分布の基本性質の1つ目は「左右対称な釣鐘型の分布」であることです。
山の頂上にあたる部分が分布の平均μになっており、そこから左右対称に裾が伸びる形をしています。
裾の広さは、標準偏差σの大きさによって変わります。
例として、平均μ=0と固定して、標準偏差の大きさを変化させた正規分布の図を3つ重ねてみたいと思います。
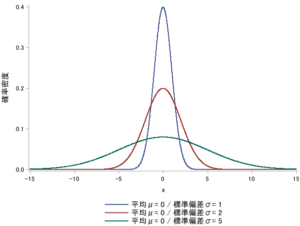
3つのグラフはそれぞれ山の高さは異なっていますが、標準偏差が小さいと裾は狭くなり、標準偏差が大きいと裾が広くなっていることが分かると思います。
ちなみに、青色の線で描かれている平均が0、分散が1(標準偏差も1)の正規分布は” 標準正規分布 ”と呼ばれます。
2. 「平均±標準偏差」で全体の何%を占めるかが分かる
1つ目の特徴で、正規分布は「平均を中心として、左右対称に裾が広がる」形をしているという説明をしましたが、その特徴を利用することで、ある範囲内に入っている人が何%程度を占めているのかが分かります。
例えば、平均を中心として左右に標準偏差1個分を取った範囲は、分布全体の約68%を占めるという性質があります。
これは、正規分布が「左右対称な分布」であるからこその性質です。
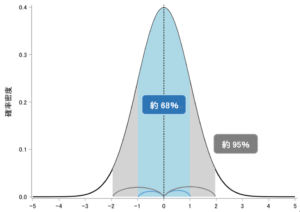
特に、平均を中心として標準偏差1.96個分の範囲は、分布全体の95%を占めることが知られており、仮説検定などでも頻発に使われる性質なので、「平均±1.96×標準偏差」という表記は覚えておくと便利です。
3. 積分を使った「分布の面積」が確率になる
2つ目の性質で、「平均を中心として左右に標準偏差1個分を取った範囲は、分布全体の約68%を占める」という話をしましたが、この68%という数字はどのように算出しているのでしょうか。
ここで、少し高校数学の知識が必要になりますが、正規分布の確率密度関数を指定した範囲で積分した値を用いることで、ある範囲に値が含まれる確率がいくつかということが分かります。
2つ目の性質もこの積分計算によって算出された値なのですが、積分範囲を変えることで平均を中心としなくても、ある範囲に値が含まれる確率が自由に算出できるようになります。
例えば、平均μが50、標準偏差σが10である正規分布に従う偏差値の分布について、偏差値60~70に含まれる確率を知りたい場合には、「標準化」と呼ばれる標準正規分布への変換を行った後に、偏差値60~70に相当する範囲で積分することで、分布の面積を求めることができます。

その後、正規分布表などを用いることで確率が算出されます。
手計算で確率を求めるのは中々大変ですが、まずは
「標準化と呼ばれる過程を経て、確率密度関数を積分することで分布の面積が求まる」、
「分布の面積によってある範囲に含まれる確率が求まる」という2つの重要な性質を覚えておくと良いでしょう!
日常生活のあらゆる所に正規分布がある?
正規分布は、英語でNormal distributionと表記され、「一般的な分布」と言われています。
その名の通り、正規分布は日常生活のあらゆるところに存在しているのです。
正規分布であることを利用すれば、多くの物事が起こる確率を計算したり、予測に使うことができます。
ここからは、正規分布が使われている身近な例を3つご紹介します!
身近な例①身長の分布
「うちのクラスの平均身長は低いけど、向こうのクラスはみんな身長が高い!」なんて場面に遭遇したことはありませんか?
学校のクラスのような少人数の単位では身長の高さにばらつきがあると思いますが、実は、日本全国の同じ年齢、同じ性別の身長を集計すると正規分布に近い分布を取るということが分かっています。
身長の分布が正規分布に近い形をしていることを仮定すれば、「身長180cm以上の17歳男性が何%程度いるか」ということも簡単に分かるので、とても便利ですよね!
身近な例②サイコロもたくさん振れば正規分布
サイコロは1から6の目がそれぞれ1/6の均等な確率で出る、というのはよく知られていることだと思います。
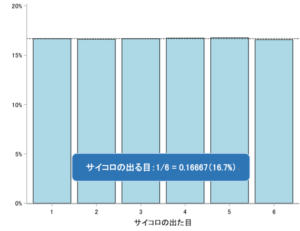
しかし実は、サイコロを複数回振った時の「出た目の平均の分布」は正規分布に従います。
例として、サイコロを3回振った時の出た目の平均の分布をヒストグラムに表してみます。
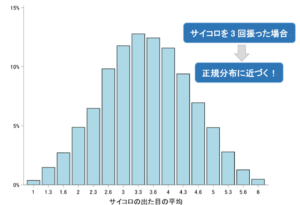
確かに正規分布に近い形になっていませんか?
これは、試行回数を増やすことで平均の分布が正規分布に近似されるという「中心極限定理」によるものなのですが、少し複雑な話になってくるので、中心極限定理についての解説はまたの機会にしたいと思います!
身近な例③イノベーター理論にも
経済学やマーケティングの分野でよく見かけるイノベーター理論も、実は正規分布に基づいた理論です!
イノベーター理論は、商品やサービスを購入するまでの時間や、市場に浸透するまでの過程を5つに分類して、どんな特徴を持つ人が多いのかということを分析したものですが、正規分布を用いることで、5つのパターンを分かりやすく示すことができるようになります。
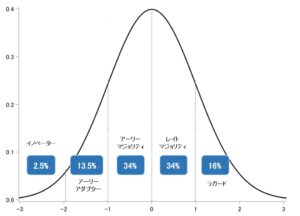
上の図の正規分布に沿って考えると、新しいものはすぐにでも試したい「イノベーター」は全体の2.5%で、イノベーターほどではないが、新商品のチェックは欠かさず、最新の情報を基に商品を購入する「アーリーアダプター」は全体の13.5%となります。
また、アーリーアダプターの評価を見てから行動を始める「アーリーマジョリティ」は全体の34%で、自分の周りで新商品を持ち始める人が増えると自身も購入を考え始めるのが、こちらも全体の34%を占める「レイトマジョリティ」です。
アーリーマジョリティとレイトマジョリティを合わせると全体の68%となるので、先ほど紹介した平均±標準偏差1個分の範囲とちょうど同じになりますね!
最後が全体の16%を占める、自分に必要なもの以外は買わないという価値観を持った「ラガード」です。
正規分布の性質を知ると、経済やマーケティングの分野の話も理解しやすくなりそうですね!
まとめ
今回は、統計学でよく耳にする「正規分布」について、その性質や身近な例について紹介しました。
数式だけを見ると複雑で難しいと感じてしまいがちですが、実は日常生活の様々なところで正規分布が使われているということを感じてもらえたら嬉しいです。
正規分布は、これから統計学の勉強をしていくうえでとても重要な分布になっていくので、基本的な性質についてはしっかりと覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





