2018年にビッグデータ利活用元年と言う言葉も出たほど、データ活用の重要性が増している現代です。
重回帰分析や主成分分析、因子分析など、様々なデータ分析の方法がありますが、正しいデータ分析を行うためには、まず分析するデータの種類を見極めることが大切になってきます。
そこで今回はデータの種類について、特に「量的データと質的データの違い」に重点をおいて分かりやすく解説していきます。
※ちなみに、量的データは「量的変数」、質的データは「質的変数」と呼ぶこともありますので、この呼び方も覚えておきましょう。
データの種類
データ分析で利用されるデータには様々な種類がありますが、大きく分けると、以下の通りに分類することが出来ます。
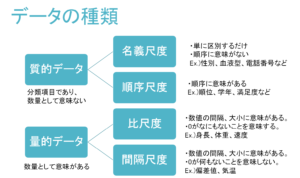
それぞれ細かく見ていきましょう!
質的データ
質的データは、カテゴリを数値に直したものです。
また、分類項目であり、数量として意味のないものという特徴もあります。
そんな質的データですが、さらに順序尺度と名義尺度の2種類に分かれます。
順序尺度
順序尺度は、順序に意味がある分類のことです。
たとえば、アンケートでよく見かける以下のような選択肢
1.大変良い 2.良い 3.どちらとも言えない 4.悪い 5.大変悪い
「大変良い」の前についている数値「1」は、「大変良い」というカテゴリを1と数値に置き換えているだけです。
そしてこの場合、1に近くなるにつれて「良い」ことを意味しているため、順序に意味があると言えます。
そのため、これは順序尺度と呼びます。
そのほかでは、大学のGPA(4.優 3.良 2.可 1.不可)なども順序尺度の代表例ですね。
また、順序尺度の数値は、計算しても意味はありません。
たとえば、GPAの「2.可」と「1.不可」の数値を足しても、2.可 + 1.不可 = 3.良 とはならないですよね。
この点も注意しておきましょう。
順序尺度では、統計量として、度数、最頻値、中央値、四分位数を利用することができますが、上で説明したとおり計算に意味がないため、平均値は求めても意味がありません。(統計量として利用できない。)
名義尺度
名義尺度は、純粋な分類であり、順序に意味がない分類のことです。
カテゴリを数値化した分類ともいえます。
たとえば、以下のようなものは名義尺度ですね。
- 男性:0 女性:1
- A型:1 B型:2 O型:3 AB型:4
A型が1でB型が2なので、数値が大きいB型の方が優れている!という話にはならないことからも分かります。
これらは、アンケートなどで、集計や分析をしやすくするために、便宜的に数値に置き換えているだけです。
また、こちらも順序尺度と同様に、計算しても意味のない尺度です。
A型:1 + B型:2 = O型:3 とはなりません。
名義尺度では、統計量として度数や最頻値を利用することが出来ますが、平均値や中央値は利用できません。
量的データ
量的データは、数量として意味のあるものです。
そんな量的データですが、さらに比率尺度と間隔尺度の2種類に分かれます。
比率尺度
比率尺度の特徴は以下の通りです。
比率尺度のポイント
- 数値の間隔に意味がある。
- 数値の大小に意味がある。
- 0がなにもないことを意味する。
たとえば、
長さ30cmと10cmでは、
20cmの長さの差があり、
30cmの方が長いことを意味します。
そして、長さが0cmの場合は、長さがない状態を表します。
この点が次に説明する間隔尺度との大きな違いです。
他の例では、体重、身長、なども比率尺度の例ですね。
比率尺度では、度数、代表値(平均値、最頻値、中央値)四分位数、標準偏差、変動係数、幾何平均など様々な統計量を利用できます。
間隔尺度
間隔尺度の特徴は、以下の通りです。
間隔尺度のポイント
- 数値の間隔(数値の差)に意味がある。
- 数値の大小にも意味がある。
- 0が何もないことを意味しない。
たとえば、50℃と40℃には温度差があります。
そして、50℃の方が温度が高いということを意味します。
そして0が何もないことを意味しないという点ですが、たとえば「0℃は温度がない」というわけではないですよね。
私たち人間が水の凍る温度を0℃にしよう!と決めただけで、0℃にも温度はあります。
これが間隔尺度の大きな特徴です。
その他の例を挙げると、試験の偏差値も間隔尺度です。
間隔尺度では、度数、代表値(平均値、最頻値、中央値)四分位数、標準偏差など様々な統計量を利用できます。
尺度水準の練習問題
ここまで学んだことの振り返りとして、練習問題を用意しました。
以下のデータが、順序尺度、名義尺度、比率尺度、間隔尺度のいずれに該当するのか、考えてみましょう。
- 電話番号
- 家賃
- 方角
- 地震の震度
- 年齢
答えを出せましたか?
それでは、解答をみていきます。
・
・
・
- 電話番号 → 名義尺度。番号に数値的な意味はない。
- 家賃 → 比率尺度。数値の大小に意味はある。(ex.家賃8万は家賃5万よりも高い。)家賃0円は、お金が発生しないことを指す。
- 方角 → 名義尺度。方角は純粋な分類です。たとえば、西が東よりも優れているということはありません。性別や血液型なども名義尺度であることを考えれば分かりやすいのではないでしょうか。
- 震度 → 順序尺度。震度5は、震度3よりも揺れが大きいと言えますが、これはあくまで人間が定めた基準です。震度6は震度3の2倍の揺れという訳でもないので、コレは順序尺度です。
- 年齢 → 比率尺度。例えば、40歳の人は、20歳の人の2倍生きたということができます。
全問正解できなかった場合は、是非各尺度の定義を見直すようにしてみてください!
この部分は統計検定の3級、4級や統計調査士などでもよく問われる統計の基本ですので、この機会にしっかり覚えておきましょう!
連続データと離散データ
また、量的データは、連続データか離散データという分類も可能です。

連続データ(連続型データ)
連続データは、数えることができない連続的なデータのことです。
例えば、身長172cmと173cmの間には、172.1cmも172.000015629・・・・・cmもあるわけで、その間は分けようと思えばいくらでも分けられるようなデータですよね。
このように2つの値の間を無限に分けられるようなデータを連続データといいます。
身長や体重、時間、気温、などが連続データの例です。
離散データ(離散型データ)
離散データは、数えることが出来る飛び飛びのデータのことです。
たとえば、人数は「1人、2人、3人」と数えていきますよね。
その1人と2人の間に、1.2人、1.5人などはありません。
このように1の次は2というように数えることが出来るデータを離散データいいます。
サイコロの目や、トランプの数字、TOEICやセンター試験の点数なども離散データの例です。
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





