この記事を読むと分かること
- 統計グラフにはどんな種類があるの?
- 各統計グラフの特徴
- 統計グラフの正しい使い分け方

統計ブロガーのにっしーです!
いきなりですが、統計グラフには様々なものがあります!
そのなかでも今回は、特に基本的なグラフをまとめてみました。
統計グラフの主たる目的は、データの特徴や傾向を視覚的になるべく分かりやすく捉えられるようにすることです。
目的に適したグラフを使うことで、より分かりやすく、正確にデータの特徴を伝えることが出来るようになります。
是非この機会に各統計グラフの特徴・使い分け方を知って、ワンランク上のビジネスマンを目指してください!
統計グラフの種類一覧
主要な統計グラフには以下のようなものがあります。
| グラフの種類 | 主な用途 |
| 棒グラフ | 棒の高さで、量の大小を比較 |
| 折れ線グラフ | 量が増えているか減っているか、変化の推移を確認 |
| 帯グラフ | 構成比を比較 |
| 円グラフ | 全体における構成比を確認 |
| レーダーチャート | 複数のデータのバランスや傾向を確認 |
| バブルチャート | 3つのデータの関係性を確認 |
| 散布図 | 2つのデータの相関関係を確認 |
| 積み上げ棒グラフ | 累積データから内訳を比較 |
| ヒストグラム | ヒストグラムは、度数分布をグラフ化したもの |
| ローソク足 | 1日の取引時間中の株価の値動き(始値、終値、高値、安値)を1本のローソクの形で表現 |
| モザイク図 | クロス集計表より、各層のデータを縦棒の積み上げグラフとして表現 |
それぞれ詳しく解説していきます。
棒グラフ
棒グラフは統計グラフのなかでも特に有名かつ基本的なものなので、既にご存じの方も多いかもしれません。
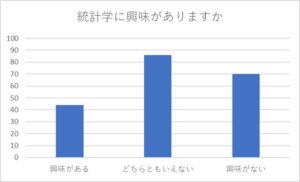
棒グラフは、棒の高さで、量の大小を比較するグラフです。
縦軸でデータ量を取っているので、高さで簡単に項目間の度数の大小を比較することが可能です。
例えば、上の棒グラフでは、統計学に興味があると回答した人よりも興味がないと回答した人の方が多いことが分かります。
折れ線グラフ
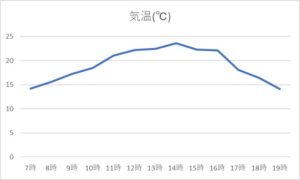
折れ線グラフは、量が増えているか減っているかといった時系列の変化の推移を確認するためのグラフです。
横軸に年月や時間などの時系列データをとり、縦軸はデータ量を取ります。
データ量を折れ線で結ぶため、下がったタイミング、上がったタイミングが一目で分かるので、ビジネスの現場では大変よく使われる重要なグラフの1つです。
ビジネスの現場では、売上や価格の推移など、定期的に追っていきたい指標の変化をみるときによく活用されます。
上の折れ線グラフでは、14時が気温のピークであることが見て取れます。
帯グラフ
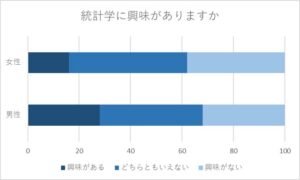
帯グラフは、複数群の項目内の構成比を比較する場合に適しているグラフです。
帯全体を100%としてしているので、各項目内で特定の値がどれくらいの割合を占めているのかを把握しやすいのが強みです。
また、複数群を並べることで、群ごとの構成比の違いの比較などが直感的に把握できます。
例えば、男女別で年代別に構成比を把握したい、アンケートの回答結果の構成比を把握したい、などで活用されます。
上の帯グラフでは、男性の方が、統計学に興味がある人の割合が高いことなどが読み取れます。
円グラフ
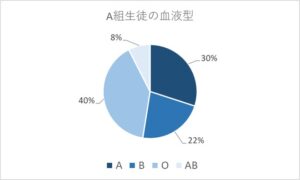
円グラフは、全体における各項目の構成比を確認するのに適したグラフです。
円全体を100%としていて、扇形の大きさで各値の割合を表します。
ただし、似たような大きさがあった時には逆に分かりにくくなるときもあるので、上図のように具体的な割合も記載しておく方が、より分かりやすくなるでしょう。
上の円グラフでは、A組の生徒の血液型の各血液型の全体における構成比を表しており、A組では、O型の生徒が40%と最も多いことが分かります。
レーダーチャート

レーダーチャートは、複数のデータのバランスや傾向を確認するのに適したグラフです。
レーダーチャートでは、表現する項目数に合わせた正多角形の形をしています。
各項目について、中心と各頂点を対応させ、中心から離れて各頂点に近いほどデータ量が大きいことを示します。
複数の項目間で、バランスがとれていれば正多角形に近い形になります。
上のレーダーチャートでは、英語が他の科目よりも値が大きいことが分かります。
バブルチャート
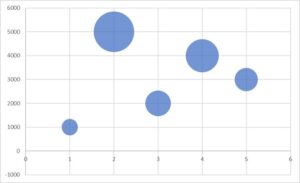
バブルチャートは、3つのデータの関係性を確認するのに適したグラフです。
バブルチャートでは、散布図のような縦横のデータに、もう一つの要素を加え、それを円の大きさで表現しています。
3つのデータの関連性をたった1つのグラフから読み取ることが出来る便利なグラフです。
例えば、「売上・客単価・客数」、「売上・利益・社員数」など様々なデータを組み合わせて確認する場合などでよく使われます。
散布図
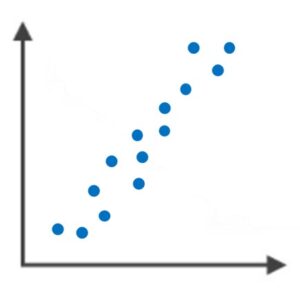
散布図は、2つのデータの相関関係を確認するのに適したグラフです。
縦軸・横軸に別のデータ量を取って、各データが該当するところに点をつけます(プロットします)。
完全な正の相関だと相関係数が1で右肩上がりの直線に、完全な負の相関ですと相関係数が-1で右肩下がりの直線となります。
また、相関関係がある=因果関係があるではないので、その点は注意が必要です。
詳しくは下記記事をご覧ください!
疑似相関(見せかけの相関)の具体例11選!~警察官が増えると検挙数が増える!?~
そのほかの注意点として、相関係数では直線的な特徴を示すので、それ以外の形で特徴的なものがあった場合でも相関はみられないとなってしまう可能性があります。
そのため、相関係数だけで判断するのではなく、合わせて散布図も確認することが大切です。
ヒストグラム
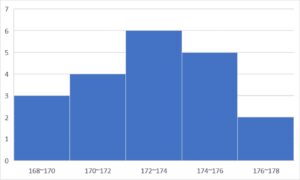
ヒストグラムは、以下のような度数分布をグラフ化したものです。
量的データの分布を把握する際によく用いられるグラフの一つです。

度数分布表に記載されたデータの分布を直感的に把握できるというメリットがあります。
たとえば、とあるクラスにおける生徒の身長の分布を知りたい場合などにヒストグラムは活用されます。
ヒストグラムでは、横軸にデータの値をとり、縦軸に度数を取ります。
見た目は少し棒グラフと似ていますが、棒グラフは分類ごとに棒が分かれているのに対し、ヒストグラムはデータの値を横軸に取っています。
横軸が連続量となるので、ヒストグラムの場合は棒グラフのように各棒の間に間隔がありません。
積み上げ棒グラフ
積み上げ棒グラフは、累積データから内訳を比較するのに適したグラフです。
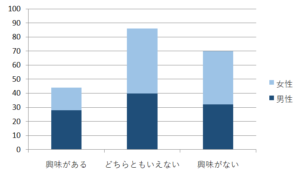
また、下記のような図は100%積み上げ棒グラフといい、いわゆる積み上げ棒グラフをそれぞれ各項目を100%としたときの割合が把握できる図です。
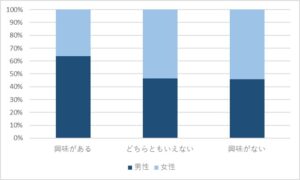
お気づきの方もおられるかもしれませんが、100%積み上げ棒グラフの役割としては先に説明した帯グラフ同じです。
(帯グラフを縦にしただけ)
ローソク足
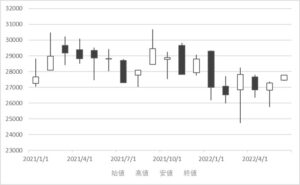
ローソク足は、1日の取引時間中の株価の値動き(始値、終値、高値、安値)を1本のローソクの形で表現した図です。
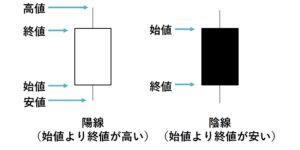
白い箱が陽線(始値より終値が高い)で、黒い箱が陰線(始値より終値が安い)を表しています。
モザイク図
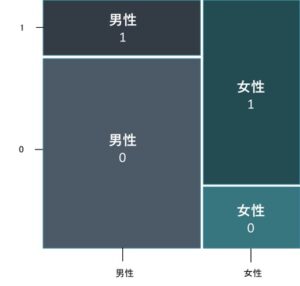
モザイク図は、クロス集計表より、各層のデータを縦棒の積み上げグラフとして表現した図です。
横幅は各層の度数の合計に比例し、四角形の面積は各セルの度数に比例した大きさとなります。
上の図は、タイタニック号の乗客の生存者・死亡者を表したモザイク図です。(正確なデータを使っておらずあくまでもイメージで作成してます。)
生存=1、死亡=0としています。
上のモザイク図より、男性の方が乗客数が多く、女性の方が生還の割合が高いことが分かります。
まとめ
グラフを正しく使えることは、プレゼンテーションの質の向上にもつながります。
デキる人のようにみえ、企画なども通りやすくなることでしょう。
是非この機会に、自分の作った資料などを見直し、適切なグラフを使えているか確認してみてください!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





