
今回は、統計学でよく使用されるジニ係数とローレンツ曲線について解説していきます。
統計調査士や統計検定2級でもよく問われる範囲なので、この機会に覚えておきましょう!
この記事を読むと分かること
- ローレンツ曲線とは
- ローレンツ曲線の読み取り方
- 均等分布線
- ジニ係数とは
- ジニ係数の求め方

最後まで楽しんで読んでいただけますと幸いです!
ローレンツ曲線
ローレンツ曲線とは
ローレンツ曲線は、アメリカの官庁統計家であるM.O.ローレンツが考案した、所得などの経済的な格差を表すグラフです。不平等さを示すグラフと表現されることもあります。
ローレンツ曲線は、横軸に世帯数の累積相対度数をとり、縦軸に所得額の累積相対度数をとって作成します。
そのため、ローレンツ曲線を描くには2つの累積相対度数が必要になります。
また、縦軸横軸ともに累積相対度数なので、グラフの軸の最小値は0、最大値は1となります。
均等分布線
グラフ上の原点を通る角度45°の対角線のことを均等分布線と呼びます。
均等分布線は完全に平等な、全く格差のない状態を表しています。
均等分布線は完全平等線と呼ばれることもあります。
ジニ係数
所得などの格差が大きいほど、ローレンツ曲線は均等分布線の下方へ膨らんでいきます。
そのため、均等分布線とローレンツ曲線で囲まれる部分の面積は、格差が大きいほど大きくなります。
この均等分布線とローレンツ曲線とで囲まれる部分の面積を2倍したものがジニ係数です。
ジニ係数は0(最小値)に近ければ近いほど格差がなく平等な状態を意味し、1(最大値)に近ければ近いほど格差が大きいと解釈することができます。
ローレンツ曲線の読み取り方
次に、具体例を挙げながらローレンツ曲線の読み取り方について説明していきます。
下のような、3つの会社の従業員の給与を例に考えていきましょう。
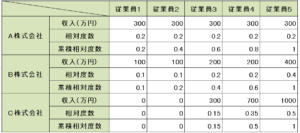
まずは、A株式会社について。 上の表から、5人が全員300万円ずつもらっていることがわかります。
この場合、全員が同じ金額をもらっているので、完全な平等だといえます。
つまり、ローレンツ曲線は均等分布線と全く同じになるというわけです。

均等分布線とローレンツ曲線が同じということは、面積も0になり、すなわちジニ係数も0、ということですね。
次に、B株式会社で働く社員の給料を考えます。 100万円が2人、200万円が2人、400万円が1人ということで、先ほどよりも所得に格差がありますね。
これをローレンツ曲線にすると下の図のようになります。
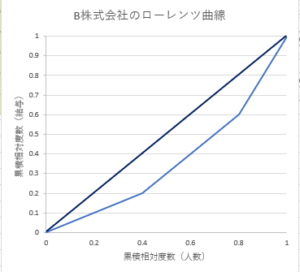
ジニ係数を求めると、0.28となりました。
(求め方は後ほど) 最後に、C株式会社では、0円が2人、300万円が1人、700万円が1人、1000万円が1人ということで、これまでよりも格差が大きそうな気がしますね。
実際にローレンツ曲線を書いてみると、下の図のようになりました。
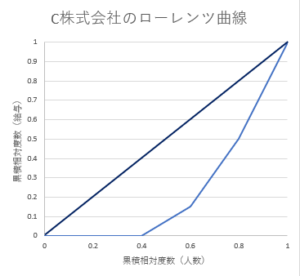
明らかにこれまでの2つよりも、下側に大きく膨らんでいることが分かります。
ジニ係数を求めると、0.54となり、A株式会社、B株式会社よりも大きくなることが分かります。
よって、所得格差の大きい順に並べると、 C > B > A ということになります。
このように所得の不平等さを視覚的に捉えることができるのがローレンツ曲線の特長であり、 その不平等さの度合いを数値で把握できるのがジニ係数の特長です。
今回は分かりやすくするために従業員5人の会社の例でしたが、 実際には、国民の世帯の所得格差などを分析する際に使用されることが一般的です。
そのため、完全平等線とローレンツ曲線が全く同じ結果になる可能性は限りなく低いです。
ジニ係数の求め方
さてここからは、先ほどのB株式会社の例を使って、ジニ係数の求め方をご紹介します。

まずは、面積を求める場所を確認しましょう。
下の図でいう、オレンジの斜線部分が、均等分布線とローレンツ曲線で囲まれた部分ですね。
この面積を求めて2倍すればジニ係数が求まるというわけです。

面積は、均等分布線より下の面積(0.5)から、細かく分割して出来る①②③のような三角形、台形の面積を引いていけば求まります。
少し手間かもしれませんが、ここは地道に求めていきましょう。
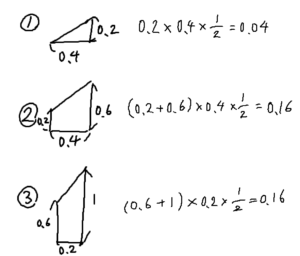
求めたら、これらを0.5から引きます。
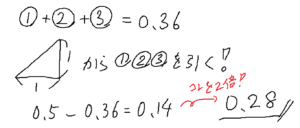
最後に2倍すれば、これがジニ係数です。
もし余裕があれば、C株式会社のジニ係数を上の手順で求めてみて、本当に0.54になるか確認してみて下さい!
まとめ
今回のポイントを簡単にまとめると、以下の通りです。
- 所得などの格差をグラフで捉えるのがローレンツ曲線、それを数値で測るのがジニ係数ということ
- ジニ係数(均等分布線とローレンツ曲線で囲まれた箇所の2倍)は0に近いほど平等、1に近いほど不平等を意味する
ローレンツ曲線とジニ係数は統計調査士の試験では、必ずと言っていいほどよく問われる定番問題です。また、統計検定2級の出題範囲でもあります。
統計に興味がある方は是非とも知っておくべき知識ですので、是非この機会に覚えておきましょう!
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





