異なる2つの数値の関連性を説明する「共分散」と「相関係数」は、統計学において非常に便利なツールとして機能しています。
しかし、共分散の概要と相関係数とのつながりを理解している方は少ないのではないでしょうか。
「共分散ってどう使うの?」
「公式が分かりづらい」
「相関係数との違いを知りたい」
そんな方もいらっしゃると思います。
そこで本記事では、共分散の概要と公式の使い方、相関係数とのつながりを解説していきます。
共分散とは

共分散(英:Covariance)とは、異なる2つのデータ値の関連性を示すものです。
通常、Cov(X,Y)またはSxyで表されます。
グラフや単なるデータの集まりだけでは分からない、両者の関連性を探ることができます。
使いこなすと非常に強力で、目にみえない部分の情報を得ることが可能になります。
数値が正、負、ゼロのとき
共分散の値が正(プラス)であるとき、片方のデータが増えると片方も増えるという関連性をみつけることができます。
反対に、共分散の値が負(マイナス)であるとき、片方のデータが増えると片方のデータが減るという関連性を得ることができます。
共分散の値がゼロであるときは、異なる2つのデータ値の関連性はなくなります。

共分散の求め方について
求め方でよく言われるのが、「2つの変数の偏差の積の平均値」です。
公式で表すと、以下の通りです。
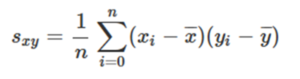
少し難しい表現なので苦戦する方もいるかと思います。
丁寧に説明すると、
![]()
この部分は、Xの値の偏差、ある値ごとの平均値との差を表します。
![]()
こちらもxと同様、値ごとの平均値との差です。
偏差の積であるため、 それぞれを掛け算して手に入るそれぞれの値を足していきます。
偏差の積を足した後、平均値を求めたいので、データ値のセット数を基に偏差の積を割ります。
偏差の積を割った後、手に入る値が共分散:Sxyとなります。
共分散を利用する例
身近な例として、身長・体重の関連性について挙げてみます。
今回は、以下のようなデータを例に考えてみましょう。
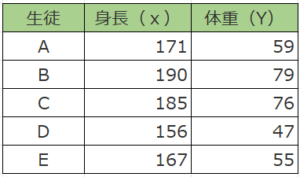
共分散を求める公式を用いて、身長・体重の関連性を求めてみましょう。
調査員が生徒ごとの身長・体重を測定しました。
身長(X)・体重(Y)の値はお互いに関連しているのか調べてみましょう。
公式
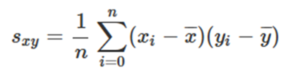
基本公式である上記の公式を扱えるようにしましょう。
複数の公式を覚えるより、基本公式を熟知して扱えるようになってください。
まず、身長(X)の平均値を求めていきます。
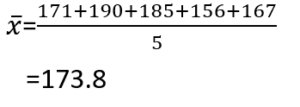
次に、体重(Y)の平均値を求めます。
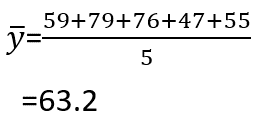
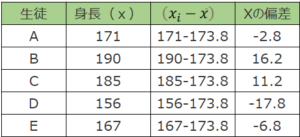
次のステップとして、身長の偏差を計算します。
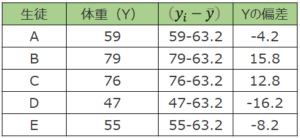
加えて、体重の偏差を計算していきます。
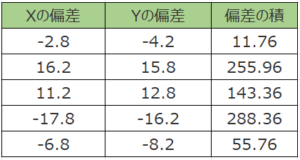
身長と体重のそれぞれの偏差の値が手に入ったので、その偏差の積たちを計算していきましょう。
次に、偏差の積を足した後、データセット数で割ります。

共分散:Sxyの値が求まりました。
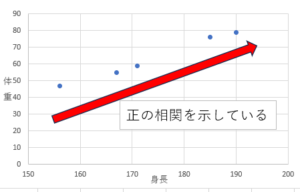
値は正を示していて、尚且つ151という大きな値です。
これは、正の関連性を強く示しており、「どちらかの値が増えると片方の値もふえる」ということを証明しています。
相関係数と共分散のつながり

相関係数は、共分散の値を用いて求めることができます。
共分散は2つのデータ値の関連性を示すものですが、値ごとに大きさが異なるため、スケールごとの関連性をイメージしづらいという欠点を抱えています。
たとえば、上記の身長・体重の共分散が「5」しかないとき、正の関連性はあるけど、どれだけ強く関連しているのか分かりづらいですよね。
そこで使われるのが相関係数になります。
相関係数は、-1 <= 相関係数 r <= 1の範囲でデータ値をとる性質を持ちます。
- 1に近い値のとき、正の関連性を示します。
- -1に近い場合は、負の関連性を示します。
- 0の場合は、関連性を示しません。
コンセプト的には共分散とほとんど同じですね。
限られた範囲だけで数値を表してくれるため、2つのデータ値の関連性を共分散よりも楽にイメージしやすいのが相関係数になります。
まとめ
当項目では共分散についての概要と公式、使い方の例と相関係数とのつながりについて紹介しました。
共分散は2つの異なるデータが関連しているのかどうかを探るために使われる、統計学的なツールです。
公式は実は単純であり、実際に例題を解きながら慣れていくことで、スムーズに公式を理解することが可能です。
正の相関、負の相関ごとにデータ値の変化の仕方を発見することができ、さまざまな科学的・社会的なフィールドで使われています。
しかし値のスケール依存が大きく、共分散の値が小さい場合、どれだけ関連しているのか分かりづらい面もあります。
そこで共分散の欠点を解消した相関係数が用いられます。
共分散も相関係数も非常に重要で、おもしろい考え方なので、ぜひこの機会を通じて慣れていってください。
(参考)
https://manabitimes.jp/math/853
https://sci-pursuit.com/math/statistics/covariance.html
https://univ-juken.com/kyobunsan
https://statisticsbyjim.com/basics/covariance/





