事柄の仮説を検証するために、統計学・法律学・社会科学などの領域において、帰無仮説と対立仮説は頻繁に利用されるテクニックです。
その中で間違った形で仮説を結論づけてしまうことを、過誤といいます。
過誤には第一種と第二種があり、それぞれ異なった意味を持ちます。
しかし名前が似ていることもあり、多くの方が混乱する項目でもあります。
「第一種の過誤と第二種の過誤の違いをしりたい!」
「有意水準とはどう繋がってるの?」
「過誤が起きてしまう例をしりたい」
このような意見を持つ方は多いと思います。
そこで本記事では、第一種の過誤と第二種の過誤の概要、有意水準との関係性、それぞれの違いについて紹介します。
第一種の過誤とは
第一種の過誤は、実際に帰無仮説が「真」である場合であっても、その仮説を「偽」として決めつけてしまう過誤のことです。
帰無仮説(検証したい仮説を否定するもの)が、その中で正しい仮説であったとしても
誤って棄却されてしまうものを指します。
概要だけでは理解することは容易ではないので、実際に例を用いて慣れていきましょう。
第一種の過誤が起きる例
過去に大流行したコロナウイルスを例にとって説明します。
科学者がコロナウイルスの感染を予防するためのワクチンを作りました。彼らは、そのワクチンがコロナ予防に効果があるのかを調べようとしています。
ここで、統計学的な検証を用いて2つの仮説を立てます。
- 帰無仮説(H₀):このワクチンはコロナ予防に効果がないとする。
- 対立仮説(H₁):このワクチンはコロナの予防に効果があるとする。
科学者達はランダムに1000人の患者に対して実験を行いました。統計的な検証の結果、そのワクチンがコロナに効果があるとして結論付けられました。
この結果、対立仮説は「真」として受け入れられ、帰無仮説は「偽」として棄却されます。
しかし、ここで問題が発生します。
このワクチンを児童と高齢者に投与したところ、患者が重篤な状態になる事故が発生しました。
なぜなら、そのワクチンがコロナに対しては本当は効果が無かったからです。
ワクチンの実証環境は、
- 母集団が1000人と小さい
- ランダムな選定の影響で90%以上が体力のある20代
- ワクチン検証が行われた場所にばらつきがある
- そもそもワクチン濃度が一定ではない
これらの理由は、ワクチンの効果に大きな影響を及ぼすことは言うまでもありません。
特に母集団、患者の年齢、ワクチン濃度は完全な検証ミスであるといえます。
これが、第一種の過誤の例です。
第二種の過誤とは?
第二種の過誤は、実際に帰無仮説が「偽」であっても、それを「真」として受け入れてしまう過誤のことです。
帰無仮説(検証したい仮説を否定するもの)が、間違った仮説であったとしても、それを正しい仮説であると結論付けてしまう誤りになります。
第二種の過誤が起きる例
カラスを例にとって説明します。
調査隊がカラスは黒色以外の種類があるということを調べたく、東京都で1万匹のカラスを対象に検証を行いました。
ここで、2つの仮説を立てます。
- 帰無仮説(H₀):カラスは全て黒色である。
- 対立仮説(H₁):カラスは黒色以外も存在する。
検証の結果、カラスが全て黒色であると結論付けられました。
この場合、帰無仮説(H₀)が「真」として受け入れられ、対立仮説(H₁)が「偽」として考えられます。
しかし、この仮説は間違いです。なぜなら、黒色以外のカラスは存在しているからです。
アルビノのカラスや、二色以上の色を持ったカラスが現実では存在しています。
加えて、
・カラスの数え方
・東京郊外からのカラスが飛来している可能性がある
などもその検証方法で問題とされるでしょう。
これが第二種の過誤の例です。
気づいた人もいるかもしれませんが、第一種・第二種の過誤も「帰無仮説」に注目するとわかりやすくなります。
有意水準との関係性
有意水準:α(アルファ)は、帰無仮説が受け入れられるか、棄却されるかの基準になる値のことです。
基本的にα=0.05または、α=0.01として設定されます。百分率で1を100%として、それぞれ5%・1%ということになります。
帰無仮説の確立を計算してその値をp値と呼びますが、その値が有意水準を下回ったとき、帰無仮説は棄却されるというルールがあります。
反対にそのp値が有意水準をうわまった場合は、帰無仮説が受け入れられることになります。
有意水準を小さく設定した場合
有意水準「α」を小さく設定すると、第一種の過誤を生み出す可能性を少なくすることができる利点があります。
しかし、同時に問題が発生します。
有意水準が小さければ小さいほど、第二種の過誤が起きる可能性が大きくなってしまうことです。
基本的に第一種・第二種の過誤が起きる可能性を、両方小さくすることはできません。なぜなら両者は表裏一体のような関係であるからです。
そのため、仮説の検証を行う際には、第一種・第二種の過誤が起きる確率をバランス良くした方法を取る必要があります。
第一種の過誤と第二種の過誤の違い
どちらの過誤も、帰無仮説を中心にして説明すると違いがわかりやすくなります。
第一種の過誤は、

第二種の過誤は、
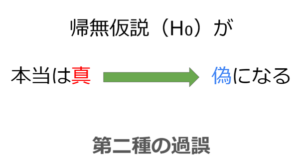
どちらの過誤も「帰無仮説の結論」が間違っているという共通点があります。
決定的な違いは、もともとの真偽の属性が
- 第一種の過誤は帰無仮説が「偽」(間違っている)
- 第二種の過誤は帰無仮説が「真」(正しい)
が、間違った仮説検証で属性が裏返ってしまうということです。
まとめ
当記事では、第一種の過誤と第二種の過誤の概要と、実際の例、有意水準との関係、それぞれの違いについて紹介しました。
第一種・第二種の過誤どちらも、仮説の検証の方法で間違った仮説を結論付けてしまうエラーになります。
似ていることもあり、学んだばかりの方は少し戸惑ってしまう項目でもあります。
しかし、「帰無仮説」に注目して過誤の種類の判断をするようにすれば、容易に理解することが可能です。
参考文献
- https://best-biostatistics.com/hypo_test/significant.html
- https://bellcurve.jp/statistics/glossary/1766.html
- https://quantcollege.net/statistics-type-1-error-and-type-2-error





