
いきなりですが、皆さんは二項分布をご存じですか。
統計学の確率分布のなかで、正規分布に次ぐほどよく出てくる分布が二項分布です。
二項分布は他の確率分布と比べてシンプルな形をしており、数学的にも理解しやすい確率分布です。
しかし、シンプルでありながら日常的な現象への応用が利きやすく、とても汎用性の高い確率分布といえます。
今回はそんな二項分布について、なるべく初心者の方でも分かりやすいように解説していきます!
是非この機会に知識を身につけておきましょう!
この記事を読むと分かること
- 二項分布とは
- ベルヌーイ試行とは
- 二項分布の確率質量関数
- 二項分布の期待値と分散
- 正規分布との違い

最後まで楽しんで読んでいただけますと幸いです!
二項分布
二項分布について理解するためには、まずその根底をなしているベルヌーイ試行についてしっかりと理解をしておく必要があります。
ベルヌーイ試行とは
ベルヌーイ試行とは、「成功か失敗か」などの2種類の結果しか得られないような試行のことです。
例えば、「コインを投げて表が出るか、裏が出るか」などが代表的な例として挙げられます。
この名前は、17世紀にこれらの試行を研究していたスイスの数学者ヤコブ・ベルヌーイから名付けられました。
そしてこのベルヌーイ試行は、以下3つの条件を満たす必要があると定義されています。
- 結果が2種類しか得られない
- 各試行は独立である(互いに影響を与えない)
- 成功確率(および失敗確率)が一定である
まず1つ目の「結果が2種類しか得られない」については、上述のとおり「失敗か成功か」「表が出るか、裏が出るか」などの2種類の結果しか得られないような状況をさしています。
そして、2つ目の「各試行は独立である」については、各試行は別な試行の結果から一切の影響を受けないことを意味しています。
例えば、コインを何度も投げて表が出るか裏が出るか観測する実験を行ったとしましょう。
この場合、ひとつ前の試行でコインを投げたときにその結果が表であろうが裏であろうが、次の試行でコインを投げたときの結果に全く関係がない、影響を及ぼさないことが直感的に理解できるかと思います。これらの各試行が影響を与え合わないことを「独立である」と表現します。
最後に、3つ目の「成功確率が一定である」については、何度も試行を行った際にその成功確率が変化しないことを示しています。
例えば上記のコインを何度も投げる実験を行う場合でいえば、同じコインを使っている限り表と裏が出る確率は変化せずに一定であることがイメージできるでしょう。
そして二項分布は、上記3つの条件を満たしているベルヌーイ試行を前提とした確率分布です。
二項分布とは
二項分布は、上記のベルヌーイ試行を何度か繰り返したときに、成功が何回起きるかを表している確率分布です。
例えば、「コインを10回投げて、表が6回出る確率」や「当選確率が15%のくじを30回やったときに3回当たりを引く確率」などについて、二項分布を使うことで調べることができます。
二項分布の確率質量関数
二項分布の確率質量関数は以下の式で表すことができます。
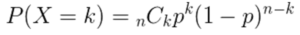
ここで、nは試行回数、kは成功回数、pは各試行で成功の結果を得る確率、1-pが失敗の結果を得る確率となります。
ベルヌーイ試行はお互いに独立しているため、成功した回数と失敗した回数でそれぞれpと1-pをその試行回数の分だけ乗算し、コンビネーションを使って組み合わせのパターンを考慮することで上記のような簡単な形で表すことができます。
例えば「コインを10回投げて、表が6回出る確率」を求める場合であれば、n=10、k=6、コインは表裏が出る確率が五分五分であるとすればp=1-p=0.5となるため、求める確率は以下のようになります。
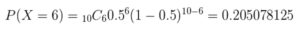
二項分布の期待値と分散
二項分布の期待値と分散は以下のようになります。
期待値
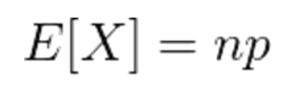
分散
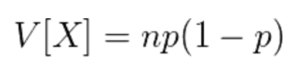
導出方法については省略いたしますが、期待値、分散ともにかなりシンプルな形で表されることがわかると思います。
例えば、「コインを連続して10回投げる実験」を考えてみましょう。
この場合は、試行回数nが10であり、成功確率pが0.5であることから、表の出る回数である確率変数Xの期待値は以下のようになります。
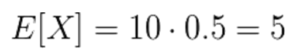
この結果が意味するところは、コインを10回投げる実験をした場合は平均的に5回表がでることが期待できるということです。
正規分布との違い
統計学においては、二項分布と並んで有名な確率分布の一つに正規分布があげられます。
正規分布は連続的な変数に関する確率分布であり、二項分布は離散的な変数に関する確率分布であるため、両者には明確な違いがあります。
しかし、二項分布は試行回数nが十分大きいとき、正規分布で近似できることがわかっています。
この法則はド・モアブル-ラプラスの定理として知られており、標準化統計量Zを用いて以下のようにあらわされます。
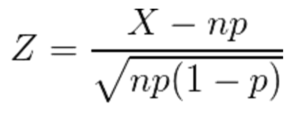
また、この近似を用いることで試行回数がとても大きい実験などについて計算が容易になります。
例えば、「コインを2500回投げるときに、表が1290回以上出る確率」を求めるような場合を考えてみましょう。
この場合、表が出る回数Xは二項分布に従うことになりますが、上記の確率を求めようとすると莫大な計算量をこなさなければなりません。
しかし、nが十分大きいためこの場合は正規分布で近似できることから、ド・モアブル-ラプラスの定理より標準化統計量Zが以下の通りであることがわかります。
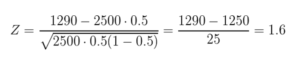
P(X≧1290)=P(Z≧1.6)であることから、標準化正規分布表で調べると求める確率は約0.055であることが簡単にわかります。
このように、二項分布は正規分布で近似することによって大きなメリットが得られます。
まとめ
今回は二項分布について解説をしました。
二項分布はシンプルかつわかりやすい形をしていますが、正規分布と組み合わせることで非常に汎用性が高くなることがわかると思います。
まさに、統計学においては欠かすことのできない重要な確率分布であるといえるでしょう。
参考サイト)https://manabitimes.jp/math/1107
↓この記事を読んだ方の多くは、以下の記事も読んでいます。





