こんにちは!統計ブロガーのにっしーです!
この記事では不偏分散の解説をします。
不偏分散は母平均がわからないときに、標本から得られた推定量から母分散を推定するときに使われます。
この記事を読むと、以下のことがわかるようになります!
この記事を読むと分かること
- 不偏分散とは
- 標本分散と不偏分散の違い
- 不偏分散では、n-1で割る理由
是非、最後まで楽しんで読んでいただければ幸いです!
分散とは
不偏分散の話に入る前に、そもそも分散とはなんでしょうか。
分散はデータがどれだけ散らばっているかを測定する統計量です。一般的に分散は以下のように定義されます。
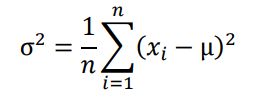
ここで、μは平均値、xiは個々のデータ、nはデータの個数を表します。
分散は、平均値μをとの差の二乗の平均で表され、データのばらつきが大きいほどその値も大きくなります。データを分析するときは、平均値だけでなく、分散も見ることでデータの集合をより深く理解できるようになります。
不偏分散とは
次に、不偏分散について解説します。
ここでは、母平均も母分散も未知であるとします。まず、母集団からランダムにn個のデータを取り出し、標本を作ります。
このとき、標本平均は、
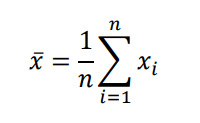
と定義されます。
この標本平均を用いて不偏分散は、以下のように定義されます。
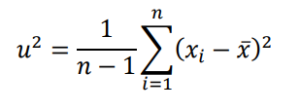
ここで、不偏分散では、「n-1」で割っていることに気をつけてください。この値は、自由度といいます。
とても重要な概念なので後半の「なぜn-1で割るのか」の項で説明します。
標本分散とは
先ほどと同様に母平均と母分散が未知の母集団からn個データを取り出すとします。そうすると、標本分散は以下のように定義されます。
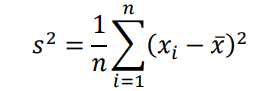
標本分散は、不偏分散と異なり、nで割っていることが特徴です。
一見、標本分散の方が扱いやすいのではと思う人も多いでしょう。実際に、先ほど示した分散の定義とよく似ています。
しかし、標本分散は以下で説明するようにある扱いづらい特徴があります。
標本分散と不偏分散の違い
標本分散と不偏分散はどう違うのでしょう。
そもそも、なぜ標本の平均や分散を求めたのでしょうか。それは、標本から母平均や母分散のような母集団の統計量を推定したいからでしたね。
標本から得られた値から母集団の統計量を推定するには以下の2つの性質を満たす必要があります。
- 一致性:標本の推定量は、取り出すデータ量が多ければ多いほど、母集団の統計量に近づく。
- 不偏性:標本の推定量の期待値が、母集団の統計量に一致する。
一致性が必要なのは、直感的にもわかりやすいのではないでしょうか。例えば、日本人全体の平均身長を調べたいときには、100人の日本人の身長をランダムで測定するより、1万人の日本人の身長をランダムで測定する方が、正確な値が出ます。
この一致性の性質は、標本分散も不偏分散も持っています。つまり、一致性の有無だけでは両者に違いはありません。
大事なのは、次の不偏性です。不偏性は標本の推定量の期待値が、母集団の統計量に一致する性質のことです。この不偏性がないと、標本からどれだけ推定量を計算したとしても母集団の統計量とは無関係になってしまいます。
母平均が未知の場合、不偏分散はこの不偏性を満たしていますが、標本分散はこの不偏性を満たしません。標本分散の期待値は、母分散の値を過小評価してしまうからです。
標本分散の期待値が、母分散の値を過小評価していることに納得してもらうために、もう一度、標本分散と不偏分散の定義を確認します。
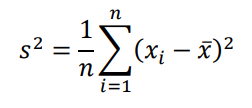
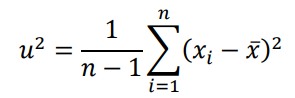
標本分散の方が、不偏分散よりも1大きい値で割り算をしていることからより小さな値になることがわかります。このことから、標本分散は母分散の値を過小評価することがわかるでしょう。
以上のことから、母平均がわかっていないときに標本から母分散を推定するには、一致性も不偏性も満たしている不偏分散が使われます。
なぜn-1で割るのか
では、なぜ不偏分散では「n-1」で割るのでしょうか。
これについて説明する前にまず、自由度の説明をします。自由度とは自分で選べる変数の数を表します。
例えば、標本平均は以下のように定義されました。
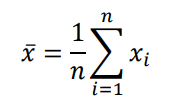
このとき、データn個の取り出し方はランダムであれば自由にとることができます。よって、「標本平均の自由度はn」といえます。
このように、自由度とは「自分で自由に決められる値の数」のことをいいます。
では、不偏分散の自由度はどうでしょうか。今一度、不偏分散の定義を確認してみましょう。
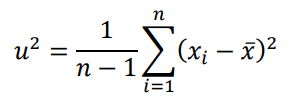
式を見ると、不偏分散の自由度はn-1です。一見、データの数がn個あるので、自由度がn個ではないかと思ってしまいます。
しかし、式中に標本平均があることが重要です。標本平均は、データの総和の値を決める値です。つまり、標本平均があることで、データの総和に制約が生まれてしまい、先ほどのようにn個のデータすべてを自由に選べません。なぜなら、最後に選ぶデータは標本平均がうまく![]() になるように調整しなければならないからです。
になるように調整しなければならないからです。
以上のことから、自由度が1つ減り、nからn-1になりました。
不偏分散の具体例な計算
最後に、不偏分散の具体的な例を考えましょう。
あるクラス30人のテスト結果が以下であったとします。

ここでは、30人すべてのデータを母集団とします
ここから無作為に5人を選び、標本を作ります。

この標本から標本分散は183、不偏分散は229であることが計算できます。
一方、母分散を計算すると、336です。合計30人のクラスで5人しか選んでいないので、標本から得られた分散と母分散の値はかなりの誤差があります。この誤差は標本の数が大きくなるほど小さくなります。
まとめ
これまで、不偏分散の説明をしてきました。
標本からは、標本分散と不偏分散の2つの分散が計算できます。母平均が未知の場合、不偏分散の方が一致性と不偏性という2つの性質を満たしているので、母分散を推定するのにより適した分散といえます。
また、不偏分散において、n-1で割る理由は、標本平均によって取り出すデータの値に制約が与えられたからでした。
最後に、具体的な例を通して、標本平均と不偏分散の計算をしました。
不偏分散は統計学の初心者がつまずきやすい概念の一つです。ぜひ、しっかり理解して標本分散と不偏分散の違いが説明できるようになりましょう。





